Cho một hình vuông có cạnh bằng 4. Chia hình vuông này thành 16 hình vuông đơn vị có cạnh bằng 1. Hỏi có bao nhiêu tam giác có các đỉnh là các đỉnh của hình vuông đơn vị?
A. 2248
B. 2148
C. 2160
D. 2168
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 5 2018
Đáp án B
Lưới hình vuông ở trên được tạo thành bởi 7 đường kẻ dọc và 5 đường kẻ ngang. Với mỗi cách chọn hai đường kẻ ngang và hai đường kẻ dọc ta thu được đúng một hình chữ nhật với các đỉnh là giao điểm của các đường đó. Từ đó suy ra số hình chữ nhật cần tìm là:
C 7 2 . C 5 2 = 210 .
AH
Akai Haruma
Giáo viên
30 tháng 6
Lời giải:
a. Gọi $x$ (m) là độ dài cạnh hình vuông được chia ($x\in\mathbb{N}$)
Theo đề ra, $x$ là $ƯC(105,75)$
Để $x$ lớn nhất thì $x=ƯCLN(105,75)$
$\Rightarrow x=15$ (m)
b.
Diện tích thửa đất: $105\times 75=7875$ (m2)
Diện tích mỗi ô vuông đất: $15\times 15=225$ (m2)
Số thửa đất ô vuông là: $7875:225=35$ (ô)
17 tháng 8 2018
Câu 1:
Chiều dài cạnh hình vuông lớn nhất là ƯCLN(53, 36) với đơn vị là m. Mà ƯCLN(53, 36) = 1 nên chiều dài cạnh hình vuông lớn nhất là 1m
11 tháng 11 2019
Bạn trình bày cho mình xem để mình đối chiếu với bài của mình với
ND
Nguyễn Đức Trí
VIP
3 tháng 8 2023
Tổng diện tích hình vuông A,C,D :
\(5.5+2.2+3.3=40\left(cm^2\right)\)
mà tấm bìa cũng là hình vuông
Nên diện tích của hình vuông B là
\(49-40=9\left(cm^2\right)\)
Diện tích hình vuông A gấp \(\dfrac{25}{9}\) lần hình vuông B
Chọn B
Số cách chọn ra 3 đỉnh trong số 25 đỉnh của các hình vuông đơn vị là: C 25 3
TH1: 3 đỉnh nằm trên cùng 1 hàng hoặc cùng 1 cột là: 5 C 5 3 + 5 C 5 3
TH2: 3 đỉnh nằm trên một trong các đường chéo của hình vuông kích thước 4x4, 3x3, 2x2 sao cho các đường chéo ấy không trùng nhau là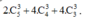
TH3: 3 đỉnh nằm trên một trong các đường chéo của hình chữ nhật kích thước 2x4. Số hình chữ nhật đó là 6. Do đó số cách chọn là 12
Vậy số tam giác được tạo thành là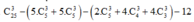
= 2148