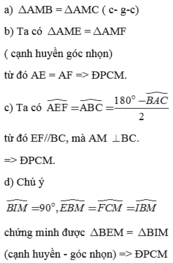
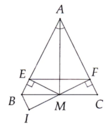
cho tam giác ABC, diểm D trên cạnh BC. Từ D kẻ các đường thẳng ss cới AB cắt AC tại E, song song với AC cắt AB tại F. chứng minh tam giác AED= tam giác DFA. chứng minh tam giác AEF= tam giác DFE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
Nguyễn Minh Quang
Giáo viên
16 tháng 12 2020
Xét tứ giác AEDF có AE//DF và AF//DE nên tứ giác AEDF là hình bình hành
do đó \(\hept{\begin{cases}AE=DF\\AF=DE\\\widehat{AED}=\widehat{DFA}\end{cases}\Rightarrow\Delta AED=\Delta DFA\left(c.g.c\right)}\)
cũng từ tứ giác AEDF là hình bình hành do đó \(\hept{\begin{cases}AE=DF\\AF=DE\\\widehat{EAF}=\widehat{FDE}\end{cases}\Rightarrow\Delta AEF=\Delta DFE\left(c.g.c\right)}\)
1 tháng 10 2021
a: Xét tứ giác BFED có
FE//BD
DE//BF
Do đó: BFED là hình bình hành
Suy ra: DE=BF
mà AE=BF
nên ED=EA
hay ΔAED cân tại E
TD
11 tháng 8 2016
a, Vì : ED//AB → ED//FB
EF//BC → EF//BD
Nên FEDB là hình bình hành → FB = ED
Mà AE = FB (gt) →AE = ED → Δ EAD là tam giác cân và cân tại E
b, Vì Δ EAD là tam giác cân tại E
nên ta có góc ADE = góc DAE(1)
VÌ DE // AB nên ta có góc ADE =góc BAD (2)
Từ (1) và (2) ta có góc DAE =góc BAD
hay AD là phân giác của góc A
CM
8 tháng 2 2018
a) Chứng minh BDEF là hình bình hành Þ ED= BF = AE Þ DAED cân ở E.
b) Ta có B A D ^ = D A C ^ (vì cùng bằng A D E ^ ) Þ AD là phân giác Â
CM
29 tháng 12 2019
Chứng minh tứ giác AEDF là hình thoi
Þ EF là phân giác của A E D ^
