Trong các hàm số dưới đây, hàm số nào đồng biến trên tập R
A. y = log 10 - 3 x
B. y = log 2 x 2 - x
C. y = e 3 2 x
D. y = π 3 x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
23 tháng 4 2019
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)
15 tháng 8 2023
Chọn D. Bởi vì hàm số ln x luôn luôn dương nên chắc chắn sẽ đồng biến trên TXĐ của nó
15 tháng 8 2023
Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
Vì \(\dfrac{1}{e}\simeq0,368< 1\)
\(\Rightarrow y=log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến trên D = \(\left(0;+\infty\right)\)
Chọn C.
13 tháng 8 2023
0<1/e<1
=>\(log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến
=>C
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
15 tháng 8 2023
Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)
CM
9 tháng 7 2017
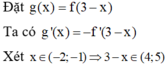
=> hàm số y=g(x) nghịch biến trên (-2; -1)
=>hàm số y=g(x) đồng biến trên (-1;2)
Chọn B