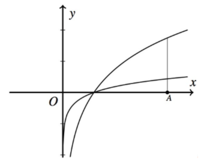
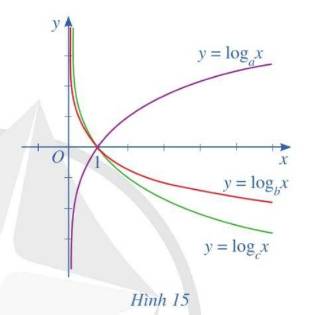
Cho hai số thực dương a, b khác 1 và đồ thị của các hàm số y = log a x , y = log b x như hình vẽ bên. Gọi d là đường thẳng song song với trục Oy và cắt trục hoành tại điểm A có hoành độ x=k(k>1) Gọi S1 là diện tích hình phẳng giới hạn bởi y = log a x , d và trục hoành; S2 là diện tích hình phẳng giới hạn bởi y = log b x , d và trục hoành. Biết S1 = 4S2. Mệnh đề nào sau đây đúng ?
A. b = a 4
B. a = b 4
C. b = a 4 ln 2
D. a = b 4 ln 2

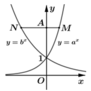
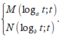
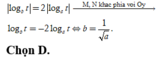
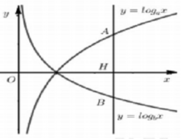
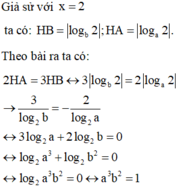
Theo giả thiết và công thức tích phân từng phần, ta có:
Vậy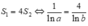
Chọn đáp án A.