Trong mặt phẳng tọa độ Oxy, các khẳng định sau đúng hay sai?
a, Hai vecto đối nhau thì chúng có hoành độ đối nhau.
b, Vecto a→ ≠ 0→ cùng phương với vecto i→ nếu a→ có hoành độ bằng 0.
c, Vecto a→ có hoành độ bằng 0 thì cùng phương với vecta j→
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong mặt phẳng tọa độ Oxy cho vectơ →a =(a1;a2) và vectơ đối của véctơ a là véctơ→b = –→a ⇒ →b = (-a1; -a2). Vật khẳng định hai véctơ đối nhau thì chúng có hoành độ đối nhau là đúng.
b) Trong mặt phẳng tọa độ Oxy véctơ →i =(1;0); Véctơ →a ≠ →0 cùng phương với véctơ→i khi a = k→i với k∈R. Suy ra →a =(k;0) với k≠0. Vậy khẳng định véctơ →a ≠ 0 cùng phương với véctơ →i nếu →a có hoành độ bằng 0 là sai.
c) Trong mặt phẳng tọa độ Oxy véctơ →j = (0;1); véctơ →a cùng phương với véctơ →j khi a = k→j với k∈R. Suy ra →a =(0;k) với k∈R. Vậy khẳng định véctơ →a có hoành độ bằng 0 thì cùng phương với véctơ →j là đúng.

a) Đúng. Giả sử A(a; b); O(0; 0) 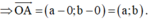
b) Đúng
c) Đúng
d) Đúng Vì tia phân giác của góc phần tư thứ nhất là đường thẳng y = x.

a.
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{2-4}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{1+5}{2}=3\end{matrix}\right.\)
\(\Rightarrow I\left(-1;3\right)\)
b.
Do C thuộc trục hoành, gọi tọa độ C có dạng \(C\left(c;0\right)\)
Do D thuộc trục tung, gọi tọa độ D có dạng \(D\left(0;d\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(c-2;-1\right)\\\overrightarrow{DB}=\left(-4;5-d\right)\Rightarrow2\overrightarrow{DB}=\left(-8;10-2d\right)\end{matrix}\right.\)
Để \(\overrightarrow{AC}=2\overrightarrow{DB}\)
\(\Leftrightarrow\left\{{}\begin{matrix}c-2=-8\\-1=10-2d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}c=-6\\d=\dfrac{11}{2}\end{matrix}\right.\)
Vậy \(C\left(-6;0\right)\) và \(D\left(0;\dfrac{11}{2}\right)\)
a) Đúng.
Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.
b) Sai.
Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.
c) Đúng.