Phát biểu định lí về dấu của tam thức bậc hai.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x = , với mọi x ≠
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).

Cách nhận biết đa thức
\(f\left(x\right)=ax^2+bx+c\)
Có nghiệm hay vô nghiệm
Lập \(\Delta\) ( đọc là delta )
\(\Delta=b^2-4ac\)
Nếu \(\Delta< 0\) : đa thức vô nghiệm
Nếu \(\Delta\ge0\) : đa thức có nghiệm
Nếu \(\Delta>0\) : đa thức có hai nghiệm
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)

Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).

5. Dấu hiệu ( định lí ) nhận biết 2 đường thẳng song song:
+ Nếu đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có 1 cặp góc so le trong bằng nhau ( hoặc góc đồng vị bằng nhau ) thì a và b song song với nhau
6. Tiên đề Ơ - clit về đường thẳng song song:
Qua 1 điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
7, Định lí về hài đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3
Nếu 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau
8. Tính chất ( định lí ) của 2 đường thẳng song song:
Nếu 1 đường thẳng cắt 2 đường thẳng song song thì
1. Hai góc đồng vị bằng nhau
2. Hai góc so le trong bằng nhau
3. Hai góc trong cùng phía bù nhau
5. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
\(\widehat{A_1}=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
\(\widehat{A}_3=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
\(\widehat{A}_2+\widehat{B}_1=180^0\Rightarrow a//b\)
a A 1 2 3 b c 1 B

- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

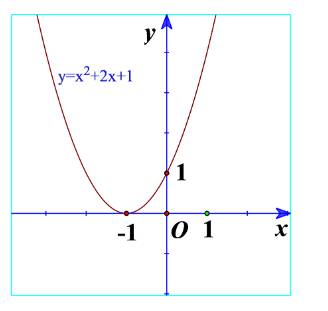
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)
Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
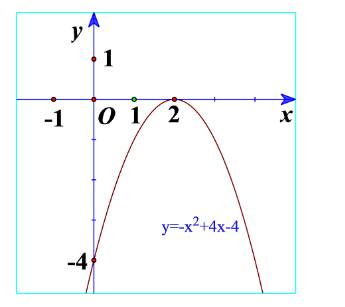
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)
Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)

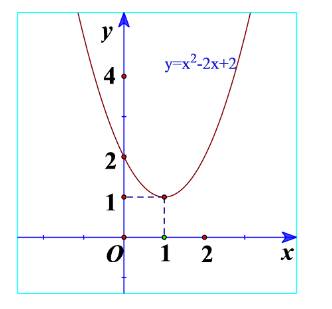
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
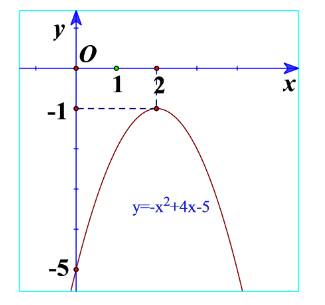
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.

- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

Định lí (trang 101 sgk Đại Số 10):
Cho tam thức f(x) = ax2 + bx + c (a ≠ 0), Δ = b2 – 4ac
- Nếu Δ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ R.
- Nếu Δ = 0 thì f(x) cùng dấu với hệ số a với mọi x ≠ -b/2a.
- Nếu Δ > 0 thì f(x) cùng dấu với hệ số a khi x < x1 hoặc x > x2
f(x) trái dấu với hệ số a khi x1 < x < x2 trong đó x1, x2 là hai nghiệm của f(x) và x1 < x2.