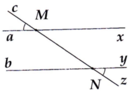
Cho hình vẽ bên, biết: a M c ^ = y N z ^ = 30 ° .
Chứng minh hai đường thẳng ax và by song song với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
CM
6 tháng 7 2019
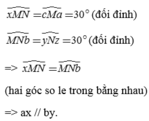
x M N ^ = c M a ^ = 30 ° (đối đỉnh), M N b ^ = y N z ^ = 30 ° (đối đỉnh)
=> x M N ^ = M N b ^ (hai góc so le trong bằng nhau) => ax // by
CM
17 tháng 12 2018
Vì Ot là phân giác A O B ^ nên:
= A O t ^ = B O t ^ = 1 2 A O B ^ = 1 2 . 60° = 30°
=> x A O ^ = A O t ^ => Ax // Ot (1)
Lại có : t O A ^ + O B y ^ = 30° +150° = 180° => Ot // By. (2)
Từ (1) và (2), ta có Ax // By // Ot
5 tháng 10 2021
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
7 tháng 12 2023
a: Xét ΔMHA vuông tại H và ΔMKB vuông tại K có
MA=MB
\(\widehat{MAH}=\widehat{MBK}\)(hai góc so le trong, AH//BK)
Do đó: ΔMHA=ΔMKB
=>MH=MK
b: Ta có: ΔMHA=ΔMKB
=>\(\widehat{HMA}=\widehat{KMB}\)
mà \(\widehat{KMB}+\widehat{KMA}=180^0\)(hai góc kề bù)
nên \(\widehat{HMA}+\widehat{KMA}=180^0\)
=>\(\widehat{HMK}=180^0\)
=>H,M,K thẳng hàng
22 tháng 9 2021
Ta có: \(\widehat{AOt}=\widehat{BOt}=\dfrac{\widehat{AOB}}{2}=60^0:2=30^0\)(do Ot là phân giác \(\widehat{AOB}\))
Ta có: \(\widehat{AOt}=\widehat{OAx}=30^0\)
Mà 2 góc này so le trong
=> Ax//Ot(1)
Ta có: \(\widehat{BOt}+\widehat{OBy}=30^0+150^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> By//Ot(2)
Từ (1),(2) => đpcm