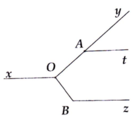
Cho hình vẽ bên, biết y A t ^ = 40 ° , x O y ^ = 140 ° , O B z ^...

PT

Pham Trong Bach

21 tháng 8 2017

Cho hình vẽ bên, biết y A t ^ = 40 ° , x O y ^ = 140 ° , O B z ^ = 130 ° và O A ⊥ O B ....

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

1

CM

Cao Minh Tâm

21 tháng 8 2017

Đúng(1)

TT

Tạ Thanh Thúy

6 tháng 11 2021

Cho hình vẽ,biết x//y;A1=40*,B1=130*.Qua điểm O vẽ z//x

a)Vì sao z//y

b)Tính AOB

#Hỏi cộng đồng OLM #Toán lớp 7

0

ZW

Za Warudo

18 tháng 7 2021

Bài 1. Cho hình vẽ bên biết AOC+BOD=140.TÍnh AOC,COB,BOD,DOA

O A D C B

Bài 3. Đường thẳng xx' cắt dường thẳng yy' từ O. Vẽ tia phân giác Ot của góc xOy

a) Gọi Ot' là tia đôi của tia Ot. So sánh xOt' và t'Oy.

b) Vẽ tia phân giác Om của góc xOy'. Tính góc mOt

#Hỏi cộng đồng OLM #Toán lớp 7

3

KS

Kinomoto Sakura

18 tháng 7 2021

Bài 1:

Vì ∠AOC = ∠BOD (đối đỉnh)

Vì ∠AOC + ∠BOD = 140^o (gt)

⇒ ∠AOC = ∠BOD = 140^o/2 = 70^o

Ta có: ∠AOC + ∠AOD = ∠COD (2 góc kề bù)

Thay số: 70^o + ∠AOD = 180^o

∠AOD = 180^o - 70^o

∠AOD = 110^o

Vì ∠AOD = ∠BOC (đối đỉnh)

⇒ ∠BOC = 110^o

Vậy ∠AOC = 70^o

∠BOD = 70^o

∠AOD = 110^o

∠BOC = 110^o

Đúng(1)

KS

Kinomoto Sakura

18 tháng 7 2021

Bài 3:

undefined

Đúng(0)

TC

Thầy Cao Đô

Giáo viên VIP

23 tháng 5 2022 - olm

Cho góc $\widehat{x O y}=140^{\circ}$. Ở ngoài của góc, vẽ hai tia $O A$ và $O B$ sao cho $O A \perp O x,$ $O B \perp O y$. Gọi $O M$ là tia phân giác của $\overline{x O y}$ và $O M'$ là tia đối của tia $OM$.

a) Chứng minh $O M'$ là tia phân giác của $\widehat{A O B}$.

b) Tính số đo góc $\widehat{xOB}$.

#Hỏi cộng đồng OLM #Toán lớp 7

1

GB

gấu béo

23 tháng 5 2022

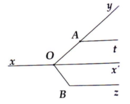
a) Ta có: $\widehat{xOy}=140^0$

$\widehat{xOA}=\widehat{yOB}=90^0$ ( do $OA\perp Ox,OB\perp Oy$ )

$\Rightarrow\widehat{AOB}=360-\left(\widehat{xOy}+\widehat{xOA}+\widehat{yOB}\right)$

$\Leftrightarrow\widehat{AOB}=360^0-\left(140^0+90^0+90^0\right)$

$\Leftrightarrow\widehat{AOB}=40^0$

$OM$ là tia phân giác của $\widehat{xOy}$

$\Rightarrow\widehat{xOM}=\widehat{MOy}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.140^0=70^0$

$OM'$ là tia đối của $OM\Rightarrow\widehat{MOM'}=180^0$

Mà $OA$ nằm ngoài $\widehat{xOy}$ và $OA\perp Ox$ nên $\widehat{MOM'}=\widehat{MOx}+\widehat{xOA}+\widehat{AOM'}$

Do đó $\widehat{AOM'}=\widehat{MOM'}-\left(\widehat{MOx}+\widehat{xOA}\right)$ $\Rightarrow\widehat{AOM'}=180^0-\left(70^0+90^0\right)=20^0$ $\left(1\right)$

Mặt khác $Oy$ nằm giữa $OB$ và $OM$ nên $\widehat{MOB}=\widehat{MOy}+\widehat{yOB}=70^0+90^0=160^0$

$\Rightarrow\widehat{MOB}< \widehat{MOM'}$

Do đó $OB$ và $Oy$ nằm cùng nửa mặt phẳng bờ $MM'$

$Ox$ nằm giữa $OA$ và $OM$ nên$\widehat{MOA}=\widehat{MOx}+\widehat{xOA}=70^0+90^0=160^0$

$\Rightarrow\widehat{MOA}< \widehat{MOM'}$

Do đó tia $OA$ và $Ox$ nằm cùng nửa mặt phẳng bờ $MM'$

Nên $OM'$ nằm giữa $OA$ và $OB$

$\Rightarrow\widehat{AOB}=\widehat{AOM'}+\widehat{M'OB}\Rightarrow\widehat{M'OB}=\widehat{AOB}-\widehat{AOM'}=40^0-20^0=20^0\left(2\right)$

Từ $\left(1\right)$ và $\left(2\right)$ ta có: $\widehat{M'OB}=\widehat{AOM'}=20^0=\dfrac{1}{2}\widehat{AOB}$

Suy ra $OM'$ là tia phân giác của góc $\widehat{AOB}$

b) Ta có: $\widehat{MOx}< \widehat{MOA}< \widehat{MOM'}$ nên $OA$ nằm giữa $Ox$ và $OM'$

Mà $OM'$ là tia phân giác của góc $\widehat{AOB}$

Suy ra $OA$ nằm giữa $Ox$ và $OB$

Vậy $\widehat{xOB}=\widehat{xOA}+\widehat{AOB}=90^0+40^0=130^0$

Đúng(4)

SP

Stellar Phan

25 tháng 9 2016

1. Biết rằng một tam giác có cả ba góc bằng nhau- Hãy cho biết số đo các góc của tam giác đó- Hãy cho biết số đo các góc ngoài của tam giác đó.2. Xem hình trên. Với hình 1, tam giác đã cho là một tam giác vuông, có một góc nhọ là x và góc nhọn kia là 50o suy ra: x + 50o = 90o hay x = 40ocho biết số đo các góc y, z, t, m trong mỗi hình vẽ ở hình...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

1

TD

Trang Đoàn

30 tháng 9 2016

Sao ko có gì vậy ạ

Đúng(0)

TQ

Tung Quan Nguyen

30 tháng 9 2016

mỹ lừa tao

Đúng(0)

TD

Trang Đoàn

29 tháng 9 2016

1. Biết rằng một tam giác có cả ba góc bằng nhau- Hãy cho biết số đo các góc của tam giác đó- Hãy cho biết số đo các góc ngoài của tam giác đó. 2. Xem hình trên. Với hình 1, tam giác đã cho là một tam giác vuông, có một góc nhọ là x và góc nhọn kia là 50o suy ra: x + 50o = 90o hay x = 40ocho biết số đo các góc y, z, t, m trong mỗi hình vẽ ở hình...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

7

TD

Trang Đoàn

29 tháng 9 2016

Toán lớp 7

Đúng(0)

NM

Nguyễn Mạnh Đạt

14 tháng 10 2016

Toán lớp 7

Đúng(0)

PT

Pham Trong Bach

29 tháng 8 2017

Cho hình vẽ bên. Tính các góc còn lại, biết a B O ^ = 140 ° , B O n ^ = 40 ° . ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

1

CM

Cao Minh Tâm

29 tháng 8 2017

Đúng(1)

KN

Kim Ngưu dễ thương

8 tháng 9 2017

tìm x,y,z, biết:

a) 5x = 8y = 20z và x-y-z = 3

b) $\dfrac{6}{11}x=\dfrac{9}{2}y=\dfrac{18}{5}z$ và -x+y+z = -120

bạn nào biết làm ơn viết lời giải ra cho mình với

#Hỏi cộng đồng OLM #Toán lớp 7

1

NM

Ngọc Minh

8 tháng 9 2017

a) 5x = 8y = 20z => $\dfrac{5x}{40}$= $\dfrac{8y}{40}$=$\dfrac{20z}{40}$=> $\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{2}$

áp dụng tính chất dãy tỉ số = nhau . Và x-y-z=3 .Ta có

$\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{2}$ =$\dfrac{x-y-z}{8-5-2}$=3

$\dfrac{x}{8}$=3 => x= 8.3

=> x = 24

$\dfrac{y}{5}=3$=> x = 5.3

=> x = 15

$\dfrac{z}{2}$=3 => x = 2.3

=> x =6

b ) ($\dfrac{6}{11}$)x = ($\dfrac{9}{2}$)y

---> x = ($\dfrac{9}{2}$)($\dfrac{11}{6}$)y = ($\dfrac{33}{4}$)y
($\dfrac{9}{2}$)y = ($\dfrac{18}{5}$)z

---> z = ($\dfrac{9}{2}$)($\dfrac{5}{18}$)y = ($\dfrac{5}{4}$)y
---> - x + y + z = ($\dfrac{-33}{4}$)y + y + ($\dfrac{5}{4}$)y = - 120
---> - 6y = - 120 ---> y = 20 ---> x = 165 và z = 25.

Đúng(0)

KN

Kim Ngưu dễ thương

8 tháng 9 2017

cảm ơn bạn nhé

Đúng(0)

NH

Nguyễn Hải An

14 tháng 11 2018

Cho X,Y,T là 3 nguyên tố liên tiếp trong 1 chu kì , tổng số hạt p của các hợp chất XH₃ , YO₂và T₂O₇ là 140 hạt . Xác định X,Y,T biết Z_T > Z_Y>Z_X

#Hỏi cộng đồng OLM #Hóa học lớp 8

1

TQ

Trương quang huy hoàng

14 tháng 11 2018

λ Hỏi đáp Hóa học

Đúng(0)

NC

Nguyễn Cẩm Tú

6 tháng 10 2021

cho hình vẽ, biết CD//Ey
góc BAx= 140 độ, góc ABD bằng 40 độ, góc BEy = 130 độ
a, tính góc CBE?
b, chứng minh Ax//Ey
c, chứng minh AB vuông góc BE thêm vào hình vẽ: A₁= 140⁰, B₁=40⁰, E₁₌130⁰
A x y E B C D

#Hỏi cộng đồng OLM #Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP