Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
Đáp án B
Ta có log(x + 2y) = log x + log y
<=> log 2 (x+2y) = log 2xy
<=> 2 (x+2y) = 2xy (*).
Đ ặ t a = x > 0 b = 2 y > 0 , khi đó
* ⇔ 2 a + b = a b
và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .
Đặt t = a + b, do đó
P ≥ f t = t 2 t + 2 .
X é t h à m s ố f t = t 2 t + 2 t r ê n [ 8 ; + ∞ )
c ó f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8
Suy ra f(t) là hàm số đồng biến trên [ 8 ; + ∞ )
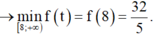
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .
\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)
a) \(log_69+log_64=log_636=2\)
b) \(log_52-log_550=log_5\left(2:50\right)=-2\)
c) \(log_3\sqrt{5}-\dfrac{1}{2}log_550=-1,0479\)
a)
Điều kiện để $1-2x > 0$ (đối số dương) là:
$1 > 2x$
$x < \frac{1}{2}$
Vậy, để biểu thức $log_3(1-2x)$ có nghĩa, giá trị của $x$ phải nhỏ hơn $\frac{1}{2}$.
\(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}=\dfrac{a^2\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{4}{5}}}{a^{\dfrac{1}{4}}}=\dfrac{a^{\dfrac{47}{15}}}{a^{\dfrac{1}{4}}}=a^{\dfrac{173}{60}}\)
\(\Rightarrow log_a\left(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}\right)=log_a\left(a^{\dfrac{173}{60}}\right)=\dfrac{173}{60}\)
\(a^{2log_a\left(\dfrac{\sqrt{105}}{30}\right)}=a^{log_a\left(\dfrac{7}{60}\right)}=\dfrac{7}{60}\)
Vậy \(B=\dfrac{173}{60}+\dfrac{7}{60}=\dfrac{180}{60}=3\)
a) \(log_29\cdot log_34=4\)
b) \(log_{25}\cdot\dfrac{1}{\sqrt{5}}=-\dfrac{1}{4}\)
c) \(log_23\cdot log_9\sqrt{5}\cdot log_54=\dfrac{1}{2}\)
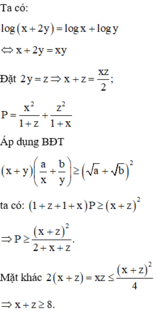
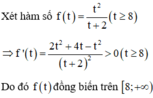
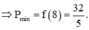
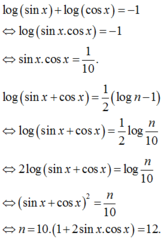
Đáp án D.
* Phương pháp tự luận:
* Phương pháp trắc nghiệm: Thay x = 2 và biểu thức P = 2 .