Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Theo giải thiết
Tập hợp điểm M là đường tròn đường kính BC.
Chọn B.
Theo giả thiết
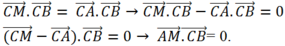
Tập hợp điểm M là đường thẳng đi qua A và vuông góc với BC.
Chọn điểm E thuộc đoạn AB sao cho EB = 2EA ⇒ 2 E A → + E B → = 0 → .
Chọn điểm F thuộc đoạn AB sao cho FA = 2FB ⇒ 2 F B → + F A → = 0 → .
Ta có
2 M A → + M B → = M A → + 2 M B → ⇔ 2 M E → + 2 E A → + M E → + E B → = M F → + F A → + 2 M F → + 2 F B →
⇔ 3 M E → + 2 E A → + E B → ⏟ 0 → = 3 M F → + F A → + 2 F B → ⏟ 0 → ⇔ 3 M E → = 3 M F → ⇔ M E = M F . ( * )
Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.
Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF
Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.
Chọn A.
Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.
Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF.
Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.
Chọn A.
Đáp án A
Gọi M a ; a 3 − 3 a suy ra PTTT tại M là: y = 3 a 2 − 3 x − a + a 3 − 3 a d
Ta có:
d ∩ Ox = B − a 3 + 3 a 3 a 2 − 3 + a ; 0
Phương trình hoành độ giao điểm của d và C là :
x 3 − 3 x = 3 a 2 − 3 x − a + a 3 − 3 a
⇔ x − a x 2 + ax + a 2 − 3 x − a = 3 a 2 − 3 x − a ⇔ x − a x 2 + a x − 2 a 2 = 0 ⇔ x − a 2 x + 2 a = 0 ⇔ x = − 2 a ⇒ A − 2 a ; − 8 a 3 + 6 a
Do A, M, B luôn thuộc tiếp tuyến d nên để M là trung điểm của AB thì:
2 y M = y A + y B
⇔ 2 a 3 − 6 a = − 8 a 3 + 6 a ⇔ 10 a 3 = 12 a ⇔ a = 0 a = ± 6 5
Do M ≠ 0 ⇒ a ≠ 0 ⇒ a = ± 6 5 .
Vậy có 2 điểm M thỏa mãn yêu cầu.
\(\Leftrightarrow\overrightarrow{CB}\left(\overrightarrow{CA}-\overrightarrow{CM}\right)=0\)
\(\Leftrightarrow\overrightarrow{CB}.\left(\overrightarrow{CA}+\overrightarrow{MC}\right)=0\)
\(\Leftrightarrow\overrightarrow{CB}.\overrightarrow{MA}=0\)
Tập hợp M là đường thẳng qua A và vuông góc BC
ĐÁP ÁN: A