Trong không gian Oxyz, cho mặt cầu (S1) có tâm I(2;1;1) có bán kính bằng 4 và mặt cầu (S2) có tâm J(2;1;5) có bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu (S1) (S1) Đặt M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm O đến (P). Giá trị M + m bằng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Do IJ =4 > R 1 + R 2 nên hai mặt cầu cắt nhau
Giả sử IJ cắt (P) tại M ta có M J M I = R 2 R 1 = 2 => J là trung điểm của MI
=> M(2;1;9) => (P): a(x-2)+b(y-1)+c(z-9)=0 a 2 + b 2 + c 2 > 0
d(I,(P))=4 ⇔ 8 c a 2 + b 2 + c 2 = 4 ⇔ 2 c a 2 + b 2 + c 2 = 1
Do đó c ≠ 0 , chọn c=1 => a 2 + b 2 = 3
Đặt a = 3 sin t , b = 3 cos t ⇒ d ( O ; ( P ) ) = 2 a + b + 9 a 2 + b 2 + c 2 = 2 a + b + 9 2 = 2 3 sin t + 3 c o s t + 9 2
Mặt khác
- 15 ≤ 2 3 sin t + 3 cos t ≤ 15 ⇒ 9 - 15 2 ≤ d 0 ≤ 9 + 15 2 ⇒ M + m = 9

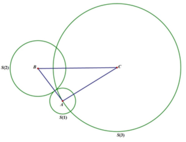
Ta dễ thấy ba điểm A, B, C thuộc mặt phẳng ![]() , 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
, 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
1. Cả 3 mặt cầu ở cùng một nửa không gian chia bởi mặt phẳng tiếp xúc. Có 2 mặt phẳng như vậy.
2. Mặt phẳng tiếp xúc chia 2 mặt cầu về một phía và phía còn lại chứa mặt cầu kia. Có 4 mặt phẳng tiếp xúc chia mặt cầu lớn và mặt cầu nhỏ ở cùng một bên. Có một mặt phẳng tiếp xúc chia 2 mặt cầu nhỏ về một bên (ở đây do R + r + d ( A, BC ) nên mới tồn tại 1 mặt phẳng tiếp xúc theo yêu cầu, nếu R + r + d > d ( A, BC ) thì sẽ tồn tại 2 mặt phẳng tiếp xúc)
Đáp án cần chọn là B

Đáp án B.
Gọi phương trình mặt phẳng cần tìm là
P : + b y + c z + d = 0.
Vì d B ; P = d C ; P = 1 suy ra
m p P / / B C hoặc đi qua trung điểm của BC.
Trường hợp 1: với
s u y r a d A ; P = 2 b + c + d b 2 + c 2 = 2
V à d B ; P = − b + c + d b 2 + c 2 = 1 ⇒ 2 b + c + d = 2 − b + c + d − b + c + d = b 2 + c 2 ⇒ 4 b = c + d c + d = 0 − b + c + d = b 2 + c 2
⇔ 3 b = b 2 + c 2 b = b 2 + c 2 ⇔ 8 b 2 = c 2 ⇒ c = ± 2 2 b c = 0 ⇒ d = 0
Suy ra có ba mặt phẳng thỏa mãn.
Trường hợp 2: Mặt phẳng (P) đi qua trùng điểm B C ⇒ P : a x − 1 + b y + 1 + c z − 1 = 0
Do đó d A ; P = 3 b a 2 + b 2 + c 2 = 2 ; d B ; P = 2 a a 2 + b 2 + c 2 = 1
Suy ra 3 b = 4 a 2 a = a 2 + b 2 + c 2 ⇔ 3 b = 4 a 3 a 2 = b 2 + c 2 ( * )
Chọn a =3 suy ra (*)
⇔ b = 4 b 2 + c 2 = 27 ⇔ b = ± 4 c 2 = 11 ⇒ a ; b ; c = 3 ; 4 ; 11 , 3 ; − 4 ; 11 3 ; 4 ; − 11 , 3 ; −...


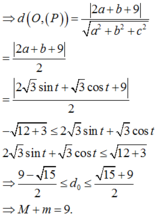







Đáp án B.
Lời giải sưu tầm :
Giả sử (P) tiếp xúc với (S1), (S2) lần lượt tại A,B
Gọi ta kiểm tra được J là trung điểm IM do
ta kiểm tra được J là trung điểm IM do 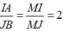 suy ra M(2;1;9).
suy ra M(2;1;9).