Thể tích của khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là :
A. V = Bh
B. V = 1 3 Bh
C. V = 1 2 Bh
D. V = 4 3 Bh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Thể tích khối lăng trụ có chiều cao h và diện tích đáy S là V = h.S
Tính toán các cạnh dựa vào định lý Pytago và hệ thức lượng trong tam giác vuông.
Cách giải:
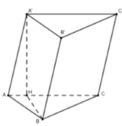
Xét tam giác vuông ABC có:
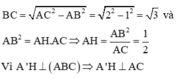


Đáp án A
Phương pháp:
Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là V = Bh
Cách giải:
Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là V = Bh

Đáp án C
Ta có thể tích của khối lăng trụ: V= h.Sđáy= 6.10 = 60 cm3→ Đáp án C

5.
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\)
\(\Rightarrow BC\perp\left(A'AM\right)\)
\(\Rightarrow\widehat{A'MA}\) là góc giữa (A'BC) và (ABC)
\(\Rightarrow\widehat{A'MA}=60^0\)
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow A'A=AM.tan60^0=\frac{3a}{2}\)
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=B.A'A=\frac{3\sqrt{3}}{8}a^3\)
1.
\(V=Bh\)
2.
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=Bh=\frac{a^2\sqrt{3}}{4}.a\sqrt{6}=\frac{3\sqrt{2}}{4}a^3\)
3.
\(B=\frac{1}{2}\left(a\sqrt{2}\right)^2=a^2\Rightarrow V=Bh=a^2.5a=5a^3\)
4.
\(h=\sqrt{\left(2a\right)^2-\left(a\sqrt{3}\right)^2}=a\)
\(B=\frac{\left(a\sqrt{3}\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}a^2\)
\(V=Bh=\frac{3\sqrt{3}}{4}a^3\)
Đáp án A