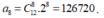Cho khai triển ( 1 + 2 x ) n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n , trong đó n ∈ ℤ + . Biết các hệ số a 0 , a 1 , . . . , a n thỏa mãn hệ thức a 0 + a 1 2 + . . . + a n 2 n = 4096 . Hệ số a 8 bằng
A. 130272
B. 126720
C. 130127
D. 213013
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(1+x\right)^n=\sum\limits^n_{k=0}C_n^kx^k\)
Hệ số của 2 số hạng liên tiếp là \(C_n^k\) và \(C_n^{k+1}\)
\(\Rightarrow7C_n^k=5C_n^{k+1}\Leftrightarrow\frac{7n!}{k!.\left(n-k\right)!}=\frac{5n!}{\left(k+1\right)!\left(n-k-1\right)!}\)
\(\Leftrightarrow\frac{7}{n-k}=\frac{5}{k+1}\Leftrightarrow7k+7=5n-5k\)
\(\Leftrightarrow5n=12k+7\Rightarrow n=\frac{12k+7}{5}\)
\(\Rightarrow n_{min}=11\) khi \(k=4\)
2/ \(\left(x-2\right)^{100}=\sum\limits^{100}_{k=0}C_{100}^kx^k.\left(-2\right)^{100-k}\)
\(a_{97}\) là hệ số của \(x^{97}\Rightarrow k=97\)
Hệ số là \(C_{100}^{97}.\left(-2\right)^3\)

Gặp dạng hệ số đằng trước giống chỉ số của số hạng thế này thì cứ đạo hàm
\(\left(1+x+x^2\right)^{20}=a_0+a_1x+a_2x^2+...+a_{40}x^{40}\)
Đạo hàm 2 vế:
\(\Rightarrow20\left(1+x+x^2\right)^{19}\left(1+2x\right)=a_1+2a_2x+3a_3x^2+...+40a_{40}x^{39}\)
Cho \(x=1\) ta được:
\(20.3^{19}.3=a_1+2a_2+3a_3+...+40a_{40}\)
\(\Rightarrow T=20.3^{20}\)

Xét khai triển:
\(\left(x+1\right)^n=C_n^0+C_n^1x+C_n^2x^n+C_n^3x^3+...+C_n^nx^n\)
Đạo hàm 2 vế:
\(n\left(x+1\right)^{n-1}=C_n^1+2C_n^2x+3C_n^3x^2+...+nC_n^nx^{n-1}\)
Thay \(x=1\) vào ta được:
\(n.2^{n-1}=C_n^1+2C_n^2+3C_n^3+...+nC_n^2=256n\)
\(\Rightarrow2^{n-1}=256=2^8\Rightarrow n=9\)
Câu 2:
\(\left(x-2\right)^{80}=a_0+a_1x+a_2x^2+a_3x^3+...+a_{80}x^{80}\)
Đạo hàm 2 vế:
\(80\left(x-2\right)^{79}=a_1+2a_2x+3a_3x^2+...+80a_{80}x^{79}\)
Thay \(x=1\) ta được:
\(80\left(1-2\right)^{79}=a_1+2a_2+3a_3+...+80a_{80}\)
\(\Rightarrow S=80.\left(-1\right)^{79}=-80\)

\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)-1\)
\(=x+\sum\limits^n_{k=2}kx\left(1+x\right)...\left(1+\left(k-1\right)x\right)\)
\(=x+\sum\limits^n_{k=2}kx\left[\left(1+x\right)...\left(1+\left(k-1\right)x\right)-1+1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left[\left(1+x\right)\left(1+2x\right)...\left(1+\left(k-1\right)x\right)-1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left(\sum\limits^{k-1}_{i=1}ix\left(1+x\right)\left(1+2x\right)...\left(1-\left(i-1\right)x\right)\right)\)
Do đó tổng của các hệ số chứa \(x^2\) là: \(\sum\limits^n_{k=2}k\left(\sum\limits^{k-1}_{i=1}i\right)\)
Hay \(a_2=\sum\limits^n_{k=2}k\left(\frac{k\left(k-1\right)}{2}\right)=\sum\limits^n_{k=2}\frac{k^2\left(k-1\right)}{2}\)
Do đó:
\(S=1+\sum\limits^{2019}_{k=2}\frac{k^2\left(k-1\right)}{2}+\sum\limits^{2019}_{k=2}k^2=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k-1\right)}{2}+k^2\right)\)
\(=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k+1\right)}{2}\right)\)


\(\left(2x+3\right)^{10}=a_0+a_1x+a_2x^2+...+a_{10}x^{10}\)
Thay \(x=1\) vào ta được:
\(5^{10}=a_0+a_1+a_2+...+a_{10}\)
Thay \(x=-1\) vào ta được:
\(\left(-2+3\right)^{10}=a_0-a_1+...+a_{10}=1^{10}=1\)

Ta có:
f ( 1 ) = \(a_0+a_1+....+a_{2017}\)
mà f ( x) = \(\left(x+2\right)^{2017}\)
=> \(S=f\left(1\right)=3^{2017}\)
Chọn B
Ta có: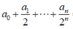
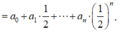
Trong khai triển ( 1 + 2 x ) n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n thay x = 1 2 ta được
Số hạng tổng quát trong khai triển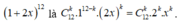
Để có số hạng chứa x 8 thì k = 8.
Vậy