Cho số phức z thỏa mãn z + z ¯ + 2 z - z ¯ = 8 ; a, b, c dương. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P = z - 3 - 3 i . Tính M + m
A. 10 + 34
B. 5 + 58
C. 10 + 58
D. 2 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi M(x; y) , F1= ( -2; 0) và F2( 2; 0).
Ta có |z + 2| + |z – 2| = 8 ![]()
Hay MF1+ MF2 = 8.
Do đó điểm M(x; y) nằm trên elip (E ) có 2a = 8 nên a = 4
ta có F1F2 = 2c nên 4 = 2c hay c = 2
Ta có b2 = a2 - c2 = 16 - 4 = 12
Vậy tập hợp các điểm M là elip 

Phương pháp:
- Tìm tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện thứ nhất.
- Tìm tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện thứ hai.
- Tìm giao hai tập hợp đó suy ra z và tính mô đun.



Đặt z=a+bi ta có z = 2 ⇔ a 2 + b 2 = 4 ( 1 )
Và ![]()
![]()
Biểu diễn (1), (2) trên cùng hệ trục toạ độ:
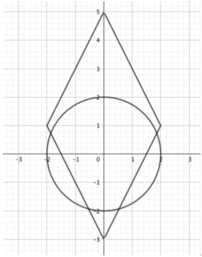
Chúng cắt nhau tại 4 điểm phân biệt, tức có 4 số phức thoả mãn.
Chọn đáp án C.
*Chú ý cách giải trên là nhanh nhất, các em có thể xét các trường hợp của trị tuyệt đối và giải hệ phương trình.
*Hình thoi trên hình vẽ được vẽ nhanh bằng cách đi tìm các đỉnh của nó, đó là giải các hệ phương trình
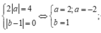
![]()
Chọn đáp án C.
Chọn đáp án B
Suy ra điểm N biểu diễn z nằm trên hình bình hành giới hạn bởi các đường thẳng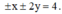 . Các đỉnh của hình bình hành là
. Các đỉnh của hình bình hành là
+ Có Hi thuộc đoạn chứa trên di tương ứng thì
với những Hi thuộc đoạn chứa trên di tương ứng