Question

[Pham Trong Bach]

Số các điểm biểu diễn nghiệm của phương trình 1 = cos x cos x + 2 sin x + 3 sin x sin x + 2 sin 2 x  trên đường tròn lượng giác là

A. 1.

B. 2

C. 3.

D. 4

Answer 1

[Cao Minh Tâm]

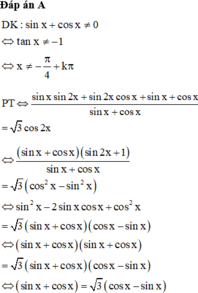
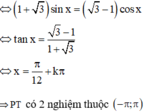
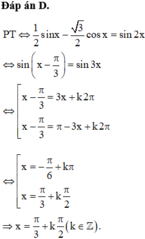
Đáp án B

Điều kiện  x ≠ π 4 + k π 2 , k ∈ ℤ   .

1 = cos x cos x + 2 sin x + 3 sin x sin x + 2 sin 2 x

⇔ sin 2 x = cos 2 x + sin 2 x + 3 sin 2 x + 3 2 sin x

⇔ cos 2 x + 3 sin 2 x + 3 2 sin x = 0

⇔ 1 − sin 2 x + 3 sin 2 x + 3 2 sin x = 0

⇔ 2 sin 2 x + 3 2 sin x + 1 = 0

⇒ sin x = 10 − 3 2 4 do  − 1 ≤ sin x ≤ 1

Vậy có hai điểm biểu diễn nghiệm của phương trình đã cho trên đường tròn lượng giác.