Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 = 3 . Một mặt phẳng α tiếp xúc với mặt cầu (S) và cắt O x , O y , O z tương ứng tại A, B, C. Tính giá trị của biểu thức T = 1 O A 2 + 1 O B 2 + 1 O C 2 .
A. T = 1 3 .
B. T = 1 3 .
C. T = 1 9 .
D. T = 3 .






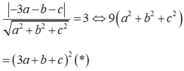
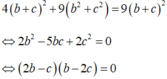
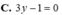


Đáp án B
Gọi α ∩ O x = A a ; 0 ; 0 α ∩ O y = B 0 ; b ; 0 α ∩ O z = C 0 ; 0 ; c ⇒ α : x a + y b + z c = 1 hay α : x a + y b + z c − 1 = 0 .
Mặt cầu (S) có tâm I = 0 ; 0 ; 0 , bán kính R = 3
Do α tiếp xúc với (S) nên d I , α = R
⇔ − 1 1 a 2 + 1 b 2 + 1 c 2 = 3 ⇔ 1 a 2 + 1 b 2 + 1 c 2 = 1 3
Suy ra T = 1 O A 2 + 1 O B 2 + 1 O C 2 = 1 a 2 + 1 b 2 + 1 c 2 = 1 3 .