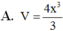
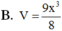
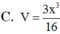
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có: S A B C = 1 2 A B . A C . sin A = a 2 3 4
Gọi M là trung điểm của B ' C ' khi đó
B ' C ' ⊥ A ' M B ' C ' ⊥ A A ' ⇒ B ' C ' ⊥ A ' M A
Suy ra A ' M A ⏜ = A B ' C ' ' A ' B ' C ' ⏜ = 30 °
Lại có A ' M = A ' B sin 30 ° = a 2 ⇒ A A ' = A ' M t a n 30 ° = a 2 3
⇒ V A B C . A ' B ' C ' = S A B C . A A ' = a 3 8
Đáp án A
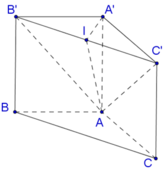
Gọi I là trung điểm của B′C′.
Trong tam giác A′B′C′ ta có
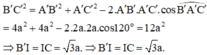
Trong tam giác A′B′I ta có
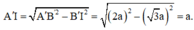
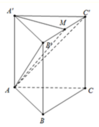
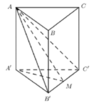
Gọi H là trung điểm BC, H' là trung điểm B'C'
\(\left\{{}\begin{matrix}AH\perp BC\\AH\perp HH'\left(HH'\cap BC=\left\{H\right\}\right)\end{matrix}\right.\Rightarrow AH\perp\left(BCC'B'\right)\)
\(\widehat{\left(ABC\right),\left(AB'C'\right)=60^0\Rightarrow\widehat{H'AH}=60^0}\)
\(AH=\dfrac{a}{2}\Rightarrow HH'=AH\tan60^0=\dfrac{a\sqrt{3}}{2}\Rightarrow V=S_{ABC}.HH'=\dfrac{1}{2}.\sqrt{3}a.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{2}=\dfrac{3a^3}{8}\)
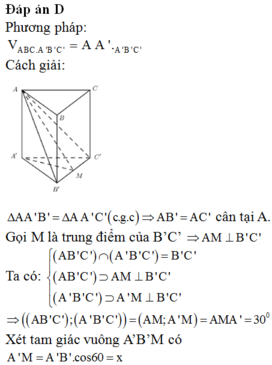
Đáp án D
Phương pháp: 
Cách giải:
=> AB’ = AC’ cân tại A
Gọi M là trung điểm của B’C’ 
Ta có: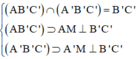 
=>((AB’C’);(A’B’C’))=(AM;A’M)=AMA’=300
Xét tam giác vuông A’B’M có A'M = A'B'. cos60 = x
Xét tam giác vuông AMA’ có: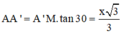
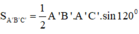
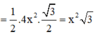
