Cho hình chóp S.ABC có đáy tam giác đều ABC cạnh là a, cạnh bên SA = a, SA ⊥ (ABC), I là trung điểm của BC. Khoảng cách giữa hai đường thẳng SI và AB là?
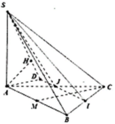
A. a 17 4
B. a 57 19
C. a 23 7
D. a 17 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

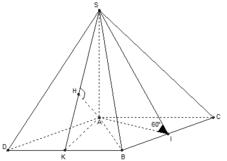
+) Hình chiếu vuông góc của SI trên mặt phẳng (ABC) là AI nên góc giữa SI và mặt phẳng (ABC) là:
(vì tam giác SIA vuông tại A nên góc SIA nhọn) ⇒ 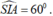
+) Xét tam giác SIA vuông tại A, 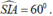
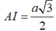 nên:
nên:
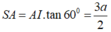
+) Dựng hình bình hành ACBD, tam giác ABC đều nên tam giác ABD đều.
+) Ta có:
AC // BD; BD ⊂ (SBD) nên AC // (SBD).
mà SB ⊂ (SBD) nên d(AC, SB) = d(A, (SBD)).
- Gọi K là trung điểm đoạn BD, tam giác ABD đều suy ra AK ⊥ BD và 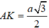 mà BD ⊥ SA nên BD ⊥ (SAK).
mà BD ⊥ SA nên BD ⊥ (SAK).
- Dựng AH ⊥ SK; H ∈ SK.
- Lại có AH ⊥ BD suy ra AH ⊥ (SBD).
- Vậy d(A, (SBD)) = AH.
- Xét tam giác SAK vuông tại vuông tại A, đường cao AH ta có:
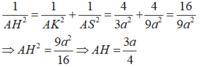
- Vậy d(AC, SB) = d(A, (SBD))
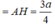

Đáp án A.
Phương pháp:
- Phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng trong không gian:
d Δ 1 ; Δ 2 = M 1 M 2 → . u 1 → ; u 2 → u 1 → ; u 2 → , M 1 ∈ Δ 1 ; M 2 ∈ Δ 2
Cách giải:
Gắn hệ trục tọa độ (như hình vẽ):
A 0 ; 0 ; 0 , B 0 ; a ; 0 , C a 3 2 ; a 2 ; 0 , S 0 ; 0 ; 3 a
M, N lần lượt là trung điểm của AB, SC
⇒ M 0 ; a 2 ; 0 , N a 3 4 ; a 4 ; 3 a 2
⇒ A N → = a 3 4 ; a 4 ; 3 a 2 ; C M → = − a 3 2 ; 0 ; 0
Đường thẳng AN có 1 VTCP u 1 → = 3 ; 1 ; 6 ,
đi qua điểm A 0 ; 0 ; 0 .
Đường thẳng CM có 1 VTCP u 1 → = 1 ; 0 ; 0 , đi qua điểm A 0 ; a 2 ; 0 .
A M → = 0 ; a 2 ; 0 , u 1 → ; u 2 → = 0 ; 6 ; − 1
d A N ; C M = A M → . u 1 → ; u 2 → u 1 → ; u 2 → = 0.0 + a 2 .6 + 0. − 1 0 2 + 6 2 + 1 2 = 3 a 37
Đáp án B
Hướng dẫn giải: Kẻ IJ // AB
Kẻ AH ⊥ SD
Ta có A D = 1 2 M C = a 3 4
Ta có 1 A H 2 = 1 A S 2 + 1 A D 2 = 19 3 a 2
⇒ A H = a 57 19