Cho hình chóp S.ABCD có S A ⊥ ( A B C ) và ∆ A B C vuông ở B. AH là đường cao của ∆ S A B . Khẳng định nào sau đây sai?
A. S A ⊥ B C
B. A H ⊥ B C
C. A H ⊥ A C
D. A H ⊥ S C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.

a: AB\(\perp\)DA
AB\(\perp\)CD
b; CD\(\perp\)BC
CD\(\perp\)AD
c: BC\(\perp\)SA
AD\(\perp\)SA

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ

Chọn C.
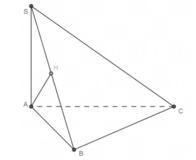
+) Do SA ⊥ (ABCD) ⇒ SA ⊥ BC nên câu A đúng.
+) Tam giác ABC vuông ở B nên AB ⊥ BC
- Lại có: SA ⊥ BC (vì SA ⊥ (ABCD))
→ Do đó: BC ⊥ (SAB) ⇒ AH ⊥ BC.
nên câu B đúng.
+) Theo trên ta có:
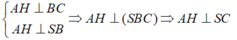
⇒ D đúng.
- Vậy câu C sai.

Chọn C.
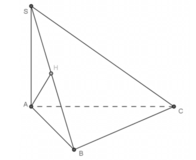
+) Do SA ⊥ (ABCD) ⇒ SA ⊥ BC nên câu A đúng.
+) Tam giác ABC vuông ở B nên AB ⊥ BC
- Lại có: SA ⊥ BC (vì SA ⊥ (ABCD))
→ Do đó: BC ⊥ (SAB) ⇒ AH ⊥ BC.
nên câu B đúng.
+) Theo trên ta có:
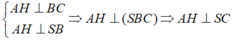
⇒ D đúng.
- Vậy câu C sai.

Đáp án C
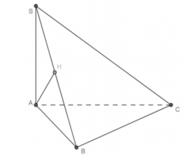
- Do SA ⊥ (ABC) nên câu A đúng.
- Do BC ⊥ (SAB) nên câu B và D đúng.
- Vậy câu C sai.
Đáp án C