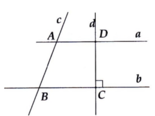
Trong hình vẽ bên, biết d vuông góc với b, B A D ^ = 100 ° v à A B C ^ = 80 ° . Chứng minh hai đường thẳng a và d vuông góc với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
5 tháng 10 2019
Đúng(1)
Những câu hỏi liên quan
PT
1
28 tháng 6 2021
b vuông góc với c và c vuông góc với d
nên b song song với d (1)
mà a vuông góc với b (2)
từ 1;2 suy ra a vuông góc với d
AH
Akai Haruma
Giáo viên
7 tháng 10 2023
Lời giải:
a.
Ta thấy $\widehat{aAb}=\widehat{ABD}=70^0$. Mà 2 góc này ở vị trí so le trong nên $a\parallel b$
b.
$\widehat{CAc}=\widehat{aAb}=70^0$ (2 góc đối đỉnh)
Vì $a\parallel b, a\perp d\Rightarrow b\perp d$
$\Rightarrow \widehat{CDB}=90^0$
14 tháng 4 2023
a, Xét tam giác ABM va Tam giác ACM :
có MB=MC (AM là trung tuyên của tam giác cân ABC)
Có AM chung
AC=AB (Tam giác ABC là tam giác cân tại A)
=>Tam giác ABM= Tam giác ACM
b:
có MK//AB => góc KMC= góc ABC (2 góc đồng vị)
mà góc ACB=góc ABC (2 góc dáy của tam giác ABC cân tại A)
=>góc KMC= góc KCM (cùng bằng góc ABC)
có AM là trung tuyến của tam giác cân ABC tại A => Am đồng thười là đg cao=> AM vuông góc vs BC tại M=> góc AMK+góc KMC =90 dộ
Có AM là đk cao của tam giác ABC tại M (CMT)
=> MAC+ MCA= 90 độ (có AM là đk cao); AMK+KMC=90 độ
mà góc KCM= góc KMC (CMT)
===> góc KAM= góc KMA (cùng phụ vs góc KMC 1 góc 90 dộ)
===> Tam giác KAM cân tại K ( điều phải chúng minh)
c;
Có AB vuông góc vs BD tại B =>góc ABD= 90*
Tương tự có Góc ACD=90*
mà góc ABC= góc ACB (CMT)
=> góc CBD= góc BCD
==> Tam giác BCD cân tại D
mà M là trung điểm của BC (giả thiết)
=> md cũng là đk cao của Tam giác cân BCD
=> góc ADM thằng hàng (định ly: có duy nhất 1 đg thằng đi qua 1 điểm và vuông góc vs đg thẳng tại điểm đó)
đây bạn ơi giúp mik nha