Cho hai đường tròn (O;R) và (O’;r). Điền vào chỗ trống của bảng sau:

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| R | r | OO’ | Hệ thức giữa OO’, R, r | Vị trí tương đối của (O) và (O’) |
| 3 | 1 | 2 | OO’ = R - r | Tiếp xúc trong |
| 3 | 1 | 4 | OO’ = R + r | Tiếp xúc ngoài |
| 3 | 1 | 3,5 | R – r < OO’ < R + r | Cắt nhau |
| 3 | 1 | 5 | OO’ > R + r | Ở ngoài nhau |
| 3 | 1 | 1 | OO’ < R - r | (O) đựng (O’) |

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD=AH*AO

a: Xét ΔABE và ΔADB co
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2=AE*AD
=>AH/AD=AE/AO
=>ΔAHE đồng dạng với ΔADO
=>góc AHE=góc ADO
=>góc OHE+góc ODE=180 độ
=>OHED nội tiếp
b: OHED nội tiếp
=>góc HED+góc HOD=180 độ
BD//AO
=>góc BDO+góc HOD=180 độ
=>góc BDO=góc HED
góc BCD+góc BDC=90 độ
góc BCD=góc BED
=>góc HED+góc BED=90 độ
=>HE vuông góc BF tại E


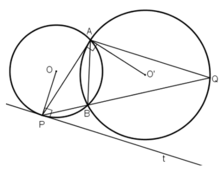
(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên:
O ’ P 2 = O ’ A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π . r 2 = 2 π ( c m 2 ) .


(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên: O ' P 2 = O ' A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π · r 2 = 2 π cm 2



Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.