Lập số có 9 chữ số, mỗi chữ số thuộc thuộc tập hợp 1,2,3,4 trong đó chữ số 4 có mặt 4 lần, chữ số 3 có mặt 3 lần, các chữ số còn lại có mặt đúng một lần. Số các số lập được là:
A. 362880
B. 120860
C. 2520
D. 15120
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Coi 9 chữ số của số được thành lập là 9 vị trí.
Chọn 4 vị trí trong 9 vị trí cho chữ số 4 có C 9 4 cách chọn.
Chọn 3 vị trí trong 5 vị trí còn lại cho chữ số 3 có C 5 3 .
Còn 2 vị trí còn lại cho chữ số 1 và 2 có 2 cách chọn.
Vậy số các số lập được là: 2. C 9 4 . C 5 3 = 2510

![]()
Xếp số vào 9 ô trống thỏa yêu cầu đề bài:
Bước 1: Chọn 2 ô trong 8 ô (bỏ ô đầu tiên) để xếp hai chữ số 0, có ![]() cách chọn.
cách chọn.
Bước 2: Chọn 3 ô trong 7 ô còn lại để xếp ba chữ số 2, có ![]() cách.
cách.
Bước 3: Chọn 2 ô trống trong 4 ô còn lại để xếp 2 chữ số 3, có ![]() cách chọn.
cách chọn.
Bước 4: Hai ô còn lại xếp 2 chữ số còn lại, có 2! Cách xếp.
Theo quy tắc nhân có: ![]()
số thỏa yêu cầu bài toán.
Chọn B.

![]()
Xếp số vào 8 ô trống thỏa yêu cầu đề bài.
Bước 1: Chọn 3 ô trong 8 ô để xếp 3 chữ số 1, có ![]() cách.
cách.
Bước 2: Chọn 2 ô trong 5 ô còn lại để xếp 2 chữ số 4, có ![]() cách.
cách.
Bước 3: Xếp 3 chữ số số còn lại vào 3 ô còn lại, có 3! cách.
Vậy có ![]() số thỏa yêu cầu, nhưng có những số có chữ số 0 đứng vị trí đầu tiên.
số thỏa yêu cầu, nhưng có những số có chữ số 0 đứng vị trí đầu tiên.
Trường hợp số 0 ở ô thứ nhất.
Bước 1: Chọn 3 ô trong 7 ô còn lại, xếp 3 chữ số 1, có ![]() cách.
cách.
Bước 2: Chọn 2 ô trong 4 ô còn lại, xếp 2 chữ số 4, có ![]() cách.
cách.
Bước 3: Xếp hai chữ số còn lại vào 2 ô còn lại, có 2! cách.
Vậy có: ![]() số mà chữ số 0 ở vị trí đầu tiên.
số mà chữ số 0 ở vị trí đầu tiên.
Kết luận có: ![]() số thỏa yêu cầu.
số thỏa yêu cầu.
Chọn C.

ta có : vì chữ số 4 có mặc 3 lần nên \(\Rightarrow\) bài toán tương đương với việc tìm số lượng của số có 7 chữ số được tạo bởi các con số : \(0,1,2,3,4,4,4\)
bước 1: tìm số lượng tất cả các số được tạo bởi bao gồm trường hợp chữ số 0 ở đầu .
ta có : số cách sắp xếp vị trí cho 3 chữ số 4 là : \(C^3_7=35\)
số cách sắp xếp vị trí cho 4 chữa số \(0,1,2,3\) là : \(P^4_4=4!=24\)
\(\Rightarrow\) có \(35.24=840\) (số)
bước 2: tìm số lượng số có chữ số 0 ở đầu
ta có : số cách sắp xếp vị trí cho 3 chữ số 4 ở 6 vị trí còn lại là : \(C^3_6=20\)
số cách sắp xếp vị trí cho 3 chữa số \(1,2,3\) ở 3 vị trí còn lại là : \(P^3_3=3!=6\)
\(\Rightarrow\) có : \(20.6=120\) (số)
\(===\Rightarrow\) số lượng số cần tìm bằng : \(840-120=720\) (số)

Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: 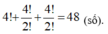
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: 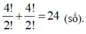
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: 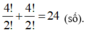
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: 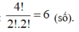
Vậy có thể lập được 102 số thỏa mãn đề bài.

| Số chữ số \(3\)\(\left(\le2\right)\) | Số chữ số \(4\) \(\left(\le2\right)\) | Số chữ số \(5\)\(\left(\le1\right)\) | Số chữ số \(6\)\(\left(\le1\right)\) | Số số tự nhiên lập được |
| 0 | 2 | 1 | 1 | 12 |
| 1 | 1 | 1 | 1 | 24 |
| 1 | 2 | 1 | 0 | 12 |
| 1 | 2 | 0 | 1 | 12 |
| 2 | 0 | 1 | 1 | 12 |
| 2 | 1 | 0 | 1 | 12 |
| 2 | 1 | 1 | 0 | 12 |
| 2 | 2 | 0 | 0 | 6 |
Ta được 12.6+24+6=102 số thỏa mãn
Đáp án C
Coi 9 chữ số của số được thành lập là 9 vị trí.
Chọn 4 vị trí trong 9 vị trí cho chữ số 4 có C 9 4 cách chọn.
Chọn 3 vị trí trong 5 vị trí còn lại cho chữ số 3 có C 5 3 .
Còn 2 vị trí còn lại cho chữ số 1 và 2 có 2 cách chọn.
Vậy số các số lập được là: 2. C 9 4 . C 5 3 = 2510