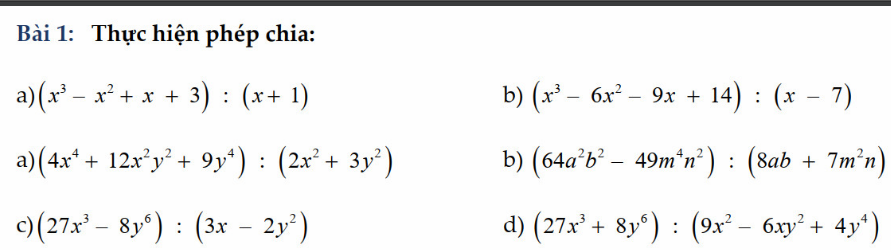 ghi là a1,a2,b1,b2 giúp e ạ
ghi là a1,a2,b1,b2 giúp e ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dễ vậy mà ko làm đc àk
\(a_1.a_2=b_1.b_2\Rightarrow\frac{a_1}{b_1}=\frac{b_2}{a_2}\)
\(\Rightarrow\frac{a_1}{b_1}+\frac{a_2}{b_2}=\frac{b_2}{a_2}+\frac{a_2}{b_2}\ge2\sqrt{\frac{b_2}{a_2}.\frac{a_2}{b_2}}=2\) (AM - GM)
có a1.a2=b1.b2
=> a1/b1=b2/a2
có \(\frac{a1}{b1}+\frac{a2}{b2}=\frac{b2}{a2}+\frac{a2}{b2}\)
áp dụng bất đẳng thức cosi cho 2 số dương có
\(\frac{b2}{a2}+\frac{a2}{b2}\ge2\sqrt{\frac{b2}{a2}.\left(\frac{a2}{b2}\right)}=2\)(đpcm)

a A 3 2 4 1 c b B 3 2 4 1
a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)

giả sử P lẻ thì a1-b2;a2-b2;a2003-b2003 lẻ.khi đó, (a1-b1)+(a2-b2)+...+(a2003-b2003) lẻ(vì có 2003 cặp số lẻ) (1)
mà (a1-b1)+(a2-b2)+...+(a2003-b2003)=(a1+a2+...+a2003)-(b1+b2+...+b2003). vì b1;b2;b3;...;b2003 là cách sắp xếp theo thứ tự khác của a1;a2;a3;...;a2003 nên (a1+a2+...+a2003)-(b1+b2+...+b2003)=0(2)
do (1) và(2) mâu thuẫn nên P ko thể là số lẻ, vậy P là số chẵn(đpcm)
tick
 nha
nha
\(a_1,=\left(x^3+x^2-2x^2-2x+3x+3\right):\left(x+1\right)\\ =\left(x+1\right)\left(x^2-2x+3\right):\left(x+1\right)\\ =x^2-2x+3\\ a_2,=\left(2x^2+3y^2\right)^2:\left(2x^2+3y^2\right)=2x^2+3y^2\\ b_1,=\left(x^3-7x^2+x^2-7x-2x+14\right):\left(x-7\right)\\ =\left(x-7\right)\left(x^2+x-2\right):\left(x-7\right)\\ =x^2+x-2\\ b_2,=\left(8ab-7m^2n\right)\left(8ab+7m^2n\right):\left(8ab+7m^2n\right)=8ab-7m^2n\\ c,=\left(3x-2y^2\right)\left(9x^2+6xy^2+4y^4\right):\left(3x-2y^2\right)\\ =9x^2+6xy^2+4y^4\\ d,=\left(3x+2y^2\right)\left(9x^2-6xy^2+4y^4\right):\left(9x^2-6xy^2+4y^4\right)\\ =3x+2y^2\)