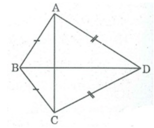
Một chiếc diều ABCD có AB = BC, AD = DC. Biết AB = 12cm, ∠ ADC = 40 ° ; ∠ ABC = 90 ° (hình bên). Hãy tính:
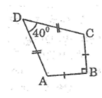
Diện tích của chiếc diều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

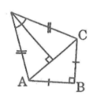
a. Nối AC và kẻ DH ⊥ AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
A C 2 = A B 2 + B C 2 = 12 2 + 12 2 = 144 + 144 = 288
Suy ra: AC = 12 2 (cm)
Ta có: ∆ ACD cân tại D
DH ⊥ AC
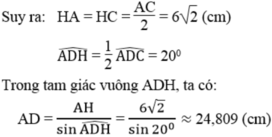

Xét ΔABC có:
.AB=BC=12cm
.\(\widehat{ABC}=90^o\)
➜ΔABC vuông cân tại B
➜AC=AB\(\sqrt{2}\) =12\(\sqrt{2}\) (cm)
Gọi H là trung điểm AC
➜AH=6\(\sqrt{2}\) (cm)
Xét ΔADC có: AD=DC
➜ΔADC cân tại D
mà: H là trung điểm AC
➜DH là đường cao, cũng là đường phân giác của ΔADC
➜\(\widehat{ADH}=20^O\)
\(\sin\widehat{ADH}=sin20^o=\dfrac{AH}{AD}\)
➜\(AD=\dfrac{AH}{\sin20^o}=\dfrac{6\sqrt{2}}{\sin20^o}=24,8\left(cm\right)\)
b, SABCD= SABC+SADC
SABCD = \(\dfrac{1}{2}.AB.BC+\dfrac{1}{2}.AC.DH\)
\(\cos\widehat{ADH}=\dfrac{DH}{AD}=\cos20^O\)
➜\(DH=\cos20^O.AD=\cos20^O.24,8=23,3\left(cm\right)\)
SABCD= \(\dfrac{1}{2}.12.12+\dfrac{1}{2}.12\sqrt{2}.23,3=269,7\left(cm^2\right)\)

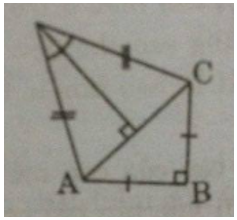
a) Nối AC và kẻ DH⊥ACDH⊥AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AC2=AB2+BC2=122+122=144+144=288AC2=AB2+BC2=122+122=144+144=288
Suy ra: AC=12√2(cm)AC=122(cm)
Ta có: tam giác ACD cân tại D
DH⊥ACDH⊥AC
Suy ra: HA=HC=AC2=6√2(cm)HA=HC=AC2=62(cm)
ˆADH=12ˆADC=20∘ADH^=12ADC^=20∘
Trong tam giác vuông ADH, ta có:
AD=AHsinˆADH=6√2sin20∘≈24,809(cm)AD=AHsinADH^=62sin20∘≈24,809(cm)
b) Ta có:
SABC=12.AB.BC=12.12.12=72SABC=12.AB.BC=12.12.12=72 (cm2)
Trong tam giác vuông ADH, ta có:
DH=AH.cotgˆADH=6√2.cotg20∘≈23,313(cm)DH=AH.cotgADH^=62.cotg20∘≈23,313(cm)
Mặt khác:
SADC=12.DH.AC≈12.23,313.12√2=197,817SADC=12.DH.AC≈12.23,313.122=197,817 (cm2)
Vậy Sdiều =SABC+SADC=72+197,817=269,817=SABC+SADC=72+197,817=269,817 (cm2)
a, nối AC rồi kẻ
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC:
Suy ra:
ta có:tam giác ABC cân tại D
Suy ra:
Trong tam giác vuông ADH, ta có
b, Ta có:
(cm2)
Trong tam giác vuông ADH, ta có:
Mặt khác
(cm2)
Vậy S (cm2)

Xét hình thang ABCD có:
AE=DE (vì E là trung điểm của AD)
BF=FC (vì F là trung điểm của BC)
=> EF là đường trúng bình của hình thang ABCD
EF=(AB+DC):2
12=(AB+16):2
24=AB+16
8=AB
=> AB=8cm

Ta có:
* BA = BC (gt)
Suy ra B thuộc đường trung trực của AC
* DC = DA (gt)
Suy ra D thuộc đường trung trực của AC
Mà B ≠ D nên BD là đường trung trực của AC
Do đó A đối xứng với C qua trục BD.

Ta có: ABCD là hình chữ nhật
nên AD=BC
hay AD=12(cm)
Ta có: ABCD là hình chữ nhật
nên AB=DC
hay DC=16(cm)
ta có: ABCD là hình chữ nhật
nên AC=BD
hay AC=20(cm)
Vậy S d i ề u = S A B C + S A D C = 72 + 197 , 817 = 269 , 817 c m 2