Cho tam giác ABC B ^ < C ^ có A ^ + 2 B ^ = 100 ° . Tính số đo A ^ + 2 B ^ .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
16 tháng 4 2019
Đúng(0)
Những câu hỏi liên quan
16 tháng 7 2019
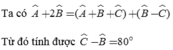
Ta có: \(\widehat{A}+2.\widehat{B}=100^0\) => \(\widehat{A}=100^0-2.\widehat{B}\)
Xét t/giác ABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(tổng 3 góc của 1 t/giác)
=> \(\left(100^0-2.\widehat{B}\right)+\widehat{B}+\widehat{C}=180^0\)
=> \(100^0-2\widehat{B}+\widehat{B}+\widehat{C}=180^0\)
=> \(100^0-\widehat{B}+\widehat{C}=180^0\)
=> \(\widehat{C}-\widehat{B}=180^0-100^0\)
=> \(\widehat{C}-\widehat{B}=80^0\)
YD
3
14 tháng 11 2019
5b
a)\(\widehat{ADC}>\widehat{ABC}\)
b)\(\widehat{BOC}>\widehat{BAC}\)
7b
Theo định lí tổng ba góc trong 1 tam giác ta có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}\)là góc tù => \(\widehat{B}>90^o\)
Tổng 3 góc trg 1 tam giác = 180 độ => A + C = 180 - B
(Giả sử góc B = 80 độ và A = C thì ta có A + C = 180 - 80 = 90 => A = C = 100/2 = 50 độ)
Từ trên suy ra góc A và góc C là 2 góc nhọn
11 tháng 4 2023
a: góc A=180/2=90 độ
b: góc OBC+góc OCB=90/2=45 độ
=>góc BOC=135 độ