Một vật có khối lượng m = 1 kg dao động điều hoà với chu kì T = 2 s. Vật qua vị trí cân bằng với vận tốc 31,4 cm/s. Khi t = 0 vật qua li độ x = 5 cm theo chiều âm quĩ đạo. Lấy π2 = 10. Phương trình dao động điều hoà của con lắc là
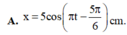
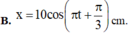

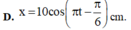
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ü Đáp án C
+ Tần số góc của dao động ω = 2 π T = π rad/s
→ Biên độ của dao động A = v m a x ω A = 10 c m
Ban đầu vật đi qua vị trí x = 0,5A = 5 cm theo chiều âm--> φ 0 = π 3
→ Phương trình dao động của vật x = 10 cos π t + π 3 c m

Đáp án A
Tần số gốc của dao động
![]()
Tốc độ của vật qua vị trí cân bằng là tốc độ cực đại
![]()
→ x = 10cos(πt – 0,5π) cm

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ Tần số góc: \(\omega = \frac{2\pi}{T}=\frac{2\pi}{2} = \pi\) (rad/s) + Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{31,4}{\pi} = 10 \ (cm)\) + t = 0 \(\Rightarrow\left\{ \begin{array}{} x_0 = 5\ cm\\ v_0 <0 \end{array} \right.\) \(\Rightarrow\left\{ \begin{array}{} \cos \varphi = \frac{5}{10}=0,5\\ \sin \varphi >0 \end{array} \right. \Rightarrow \varphi = \frac{\pi}{3}\) Phương trình dao động: \(x=10\cos(\pi t + \frac{\pi}{3})\) (cm)
Chọn C
+ ω = 2π : T = 20 rad/s.
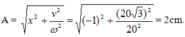
+ t = 0: x = 2cosφ = -1 => 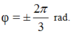
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.
Ban đầu vật đi qua vị trí x = 0,5A = 5 cm theo chiều âm
Đáp án C