Xác định vị trí trọng tâm của bản mỏng là đĩa tròn tâm O bán kính R, bản bị khoét một lỗ tròn bán kính R 2 như hình
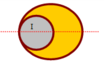
A. R 3
B. R 4
C. R 5
D. R 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tính đối xứng G nằm trên đường thẳng OO’ về phía đầy.
Trọng tâm của đĩa nguyên vẹn là tâm O; trọng tâm của đĩa bị khoét là O’.
P → là hợp lực của hai lực P → 1 , P → 2 .
O G O O ' = P 2 P 1 = m 2 m 1 = V 2 V 1 = S 2 S 1 = π R 2 4 3 π R 2 4 = 1 3 ⇒ O G = R 6

Giả sử ta khoét thêm một lỗ tròn bán kính R/2 nữa đối xứng với lỗ tròn đã khoét lúc đầu (H.III.6G)
Gọi P → là trọng lượng của đĩa bán kính R khi chưa bị khoét, P 1 → là trọng lượng của đĩa nhỏ có bán kính R/2 và P 2 → là trọng lượng của phần đĩa còn lại sau hai lần khoét, ta có:
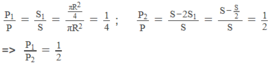
Do tính chất đối xứng, trọng tâm phần đĩa còn lại sau hai lần khoét thì trùng với tâm O của đĩa khi chưa khoét, còn trọng tâm của đĩa nhỏ mà ta giả sử khoét thêm thì ở tâm O 1 của nó. Gọi G là trọng tâm của đĩa sau khi bị khoét một lỗ tròn. Ta có hệ phương trình
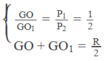
Giải ra ta được: G O 1 = R/3 và GO = R/6

![]()
Gọi x là khoảng cách từ tâm hình tròn lớn O đến trọng tâm phần còn lại O1.
Theo quy tắc hợp lực song song:
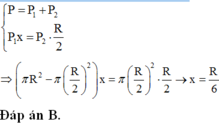

Tóm tắt:
tâm O1; R1 = 20cm. D = 120 cm
Tâm O2; R2 = 12 cm.
a) O1O2 =? Để Rtối = 4 cm. R’nửa tối =?
b) O1O2 =? Để Rtối = 0 cm
Bài giải
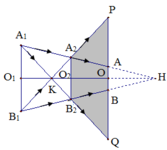
a) Từ hình vẽ ta có: OA là bán kính của vùng tối trên màn, OA = R = 4 cm
- OP là bán kính của đường tròn giới hạn ngoài cùng của vung nửa tối OP =R’
Ta có: ∆ HAO ~ ∆ HA1O1 => H O H O 1 = A O A 1 O 1 ⇔ H O H O + O O 1 = R R 1 ⇔ H O H O + D = R R 1
⇒ H O H O + D − R R 1 = 0 ⇒ H O . R 1 − H O . R = R D ⇒ H O . ( R 1 − R ) = R D ⇒ H O = R D R 1 − R
Thay số ta có HO = 4.120 20 − 4 = 480 16 = 30 cm => HO1 =120+30=150 cm
Mặt khác:
Δ H A 2 O 2 ~ Δ H A 1 O 1 => H O 2 H O 1 = A 2 O 2 A 1 O 1
=> HO2 = A 2 O 2 A 1 O 1 . H O 1 = R 2 R 1 .150 = 12 20 .150 = 90 cm.
Vậy đĩa chắn sáng phải đặt cách đĩa phát sáng một khoảng
O1O2 = HO1 – HO=90-30=60 cm thì vùng tối trên màn có bán kính là 4 cm.
Tính R’:
Ta có: Δ K A 1 O 1 ~ Δ K B 2 O 2 => K O 1 K O 2 = A 1 O 1 A 2 O 2 => K O 1 O 1 O 2 − K O 1 = R 1 R 2
⇔ K O 1 O 1 O 2 − K O 1 − R 1 R 2 = 0
⇒ K O 1 . R 2 + K O 1 . R 1 = R D ⇒ K O 1 . ( R 1 + R 2 ) = R 1 . O 1 O 2 ⇒ K O 1 = R 1 . O 1 O 2 R 1 + R 2
Thay số ta có KO1 = 20.60 20 + 12 = 1200 32 = cm => KO1 = 37.5 cm
Mặt khác:
Δ H A 1 O 1 ~ Δ K Q O ⇒ K O 1 K O = A 1 O 1 Q O ⇔ K O 1 D − K O 1 = R 1 R 1 '
=> R’= ( D − K O 1 ) . R 1 K O 1 thay số ta có:
R’ = ( 120 − 37.5 ) .20 37.5 = 44 cm.
b) Ta có hình vẽ:
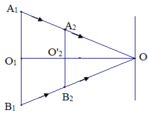
Từ hình vẽ ta có để trên nàm hình vừa vặn không còn bóng tối thì phải di chuyển đĩa chắn sáng về phía O1 một đoạn O2O’2 .
Ta có:
Δ A 2 O 2 ' O ~ Δ A 1 O 1 O n ê n O 2 ' O O 1 O = A 2 O 2 ' A 1 O 1 ⇒ O 2 ' O = O 1 O . A 2 O 2 ' A 1 O 1 = D . R 2 R 1
Thay số ta có: O 2 ' O = 120. 12 20 = 72 cm.
Mà O1O2 = OO1 - OO’2 = 120-72 = 48 cm
Nên O2O’2 = O1O2 – O1O’2 = 60-48 = 12 cm
Vậy phải di chuyển đĩa chắn sáng đi một đoạn 12 cm thì trên màn vừa vặn không còn vùng tối.


Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).
Chọn đáp án D
Do tính đối xúng → G nằm trên đường thẳng OO' về phía đầy
Trọng tâm của đĩa nguyên vẹn là tâm O; trọng tâm của đĩa bị khoét là O'