Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a và S A ⊥ ( A B C ) . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 0 . Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
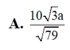
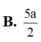
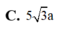

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

Do S A ⊥ A B C nên góc giữ SC và A B C là góc S C A ^ = 60 °
Vì Δ A B C vuông tại B nên A C = 5 a ⇒ S A = 5 a 3
Gọi N là trung điểm BC nên M N / / A B ⇒ A B / / S M N
d A B , S M = d A B , S M N = d A , S M N .
Từ A kẻ đường thẳng song song vơi BC cắt MN tại D.
Do B C ⊥ A B ⇒ B C ⊥ M N ⇒ A D ⊥ M N .
Từ A kẻ AH vuông góc vơi SD
Ta có M D ⊥ A D M D ⊥ S A ⇒ M D ⊥ S A D ⇒ M D ⊥ A H
Mà A H ⊥ S D ⇒ A H ⊥ S M D hay A H ⊥ s m n ⇒ d A , S M N = A H
Do A D = B N = 1 2 B C = 2 a .
Xét Δ S A D có 1 A H 2 = 1 S A 2 + 1 A D 2 = 1 75 a 2 + 1 4 a 2 = 79 300 a 2
⇒ d A B , S M = A H = 10 237 a 79 = 10 3 a 79

Gọi N là trung điểm của BC, dựng hình bình hành ABNP.
Ta có:
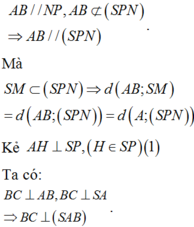
Mà
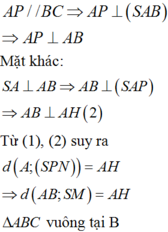
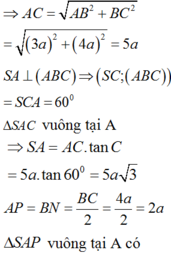
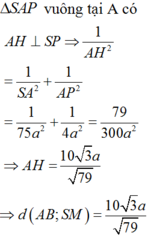
Chọn: B

Đáp án D
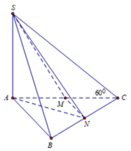
Gọi N là trung điểm của BC
Ta có A B / / M N ⇒ d A B ; S M = d A ; S M N
S A = A C tan 60 ° = 5 a 3
S M = 5 a 3 2 + 5 a 2 2 = 5 a 13 2
S N 2 = S B 2 + B N 2 = S A 2 + A B 2 + B C 2 2 = 5 a 3 2 + 3 a 2 + 2 a 2 = 88 a 2
⇒ S N = 2 a 22
M N = A B 2 = 3 a 2
Ta có:
S M 2 = N S 2 + N M 2 − 2 N S . N M . c o s M N S ^ ⇔ 5 a 13 2 22 = 88 a 2 + 3 a 2 2 − 2.2 a . 22 . 3 a 2 c o s M N S ^
c o s M N S ^ = 3 2 22 ⇒ sin M N S ^ = 79 88
S S M N = 1 2 N M . N S . s i n M N S ⏜ = 1 2 . 3 a 2 .2 a 22 . 79 88 = 3 a 2 79 4
S A M N = 1 4 S A B C = 1 4 . 1 2 .3 a .4 a = 3 a 2 2 ; V S . A M N = 1 3 S A . S A M N = 1 3 .5 a 3 . 3 a 2 2 = 5 a 3 3 2
d A ; S M N = 3 V S . A M N S S M N = 3. 5 a 3 3 2 3 a 2 79 4 = 10 a 3 79

Đáp án B
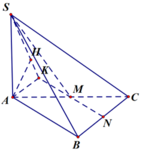
Gọi N là trung điểm của BC.
d A B , S M = d A , S M N
Dưng đường cao AK trong tam giác AMN, dựng đường cao AH trong tam giác SAK.
Dễ dàng chứng minh được A H ⊥ S M N tại H, suy ra d A B , S M = d A , S M N = A H
A K = B N = 2 a , S A = 5 a 3 ⇒ A H = 10 a 3 79

Chọn D
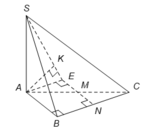
Xác định được
![]()
![]()
Gọi N là trung điểm BC, suy ra MN//AB.
Lấy điểm E đối xứng với N qua M, suy ra ABNE là hình chữ nhật.
Do đó
![]()
![]()
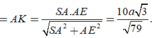

Xác định được ![]()
Khi đó ta tính được ![]()
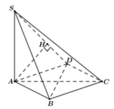
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
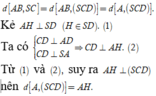
Xét tam giác vuông SAD có 
Chọn C.