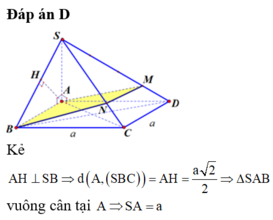
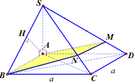
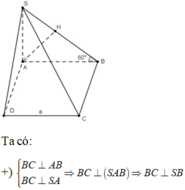
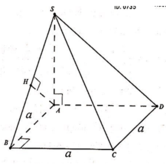
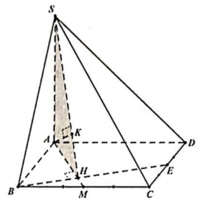
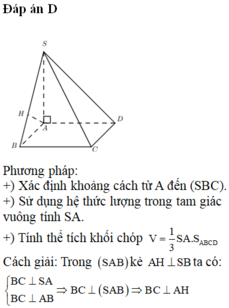
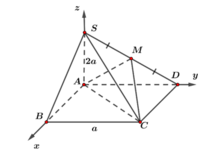
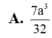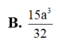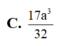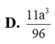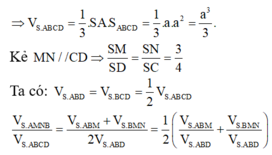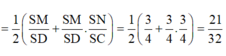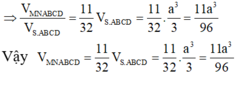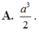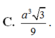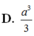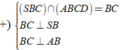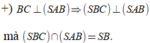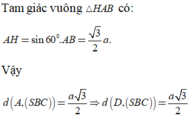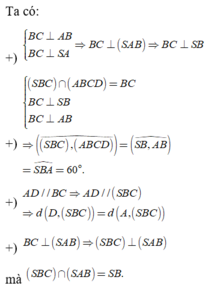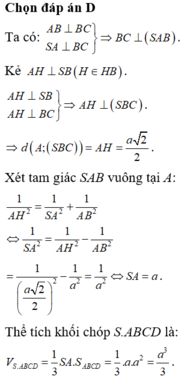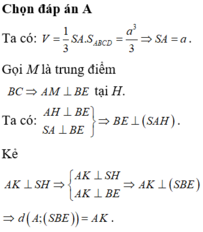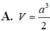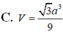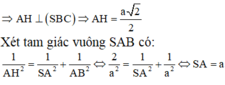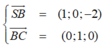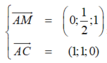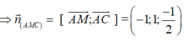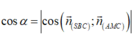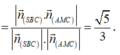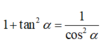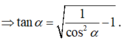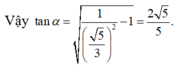Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng a 2 2 . Gọi M là điểm thuộc cạnh SD sao cho SM=2MD. Mặt phẳng (ABM) cắt cạnh SC tại điểm N. Thể tích khối đa diện MNABCD bằng