Cho đường thẳng d song song mặt phẳng ( α ) nằm trong mặt phẳng ( β ) . Gọi a là giao tuyến của ( α ) và ( β ) Khi đó
A. a và d trùng nhau.
B. a và d cắt nhau.
C. a song song d.
D. a và d chéo nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Do a là giao điểm của ( α ) và ( β ) nên a và d cắt nhau.

Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.

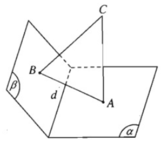
Hai mặt phẳng (α) và (β) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng, điều đó là vô lí.
Mặt khác (α) và (β) cũng không song song với nhau.
Vì nếu (α) // (β), thì từ CB ⊥ (β) ta suy ra CB ⊥ (α)
Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với (α), điều đó là vô lí.
Vậy (α) và (β) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là d = (α) ∩ (β)
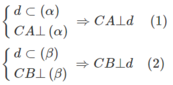
Từ (1) và (2) suy ra d ⊥ (ABC).

Hai mặt phẳng song song α và β ⇒ α và β không có điểm chung
Đường thẳng d nằm trong α ⇒ Đường thẳng d không thể cắt mặt phẳng β. Vì nếu d cắt mặt phẳng β tức là d và β có điểm chung
=> hai mặt phẳng α và β có điểm chung (mâu thuẫn với giả thiết)
Vậy d và β không có điểm chung

Sai vì
Ta có định lí 3 trang 67: cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song
Theo đề bài ta có: (α) // (β)
a//b nên A,B,C,D thuộc mặt phẳng
AB là giao tuyến của (α) và (ABDC)
CD là giao tuyến của (β) và (ABDC)
⇒ AB // CD (theo định lí)
Hình 2.72 không biểu diễn được AB // CD

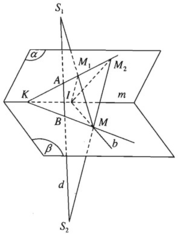
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.

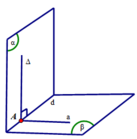
Δ nằm trong (α) và Δ vuông góc với d ⇒ Δ cắt d tại A
Từ A, vẽ đường thẳng a thuộc (β) và a ⊥ d
Khi đó góc giữa 2 mp (α) và (β) bằng góc giữa hai đường thẳng ∆ và a.
Vì (α) ⊥ (β) nên góc giữa Δ và a là 90° hay Δ ⊥ a
⇒ Δ ⊥ (d,a) hay Δ ⊥ (β)
Đáp án C
Do a là giao điểm của ( α ) và ( β ) nên a và d cắt nhau.