Cho tập X = {1;2;3;....;8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là
A . C 8 2 C 6 2 C 4 2 8 !
B . 4 ! . 4 ! 8 !
C . 384 8 !
D . A 8 2 A 6 2 A 4 2 8 !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tập hợp C rỗng vì \(x^2+7x+12=0\Leftrightarrow x\in\left\{-3;-4\right\}\notin N\)
\(a,\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\}\\ b,\left\{1\right\};\left\{2\right\};\left\{3\right\};\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\};\left\{1;2;3\right\}\)
\(X=\left\{1;3\right\}\\ X=\left\{1;2;3\right\}\\ X=\left\{1;3;4\right\}\\ X=\left\{1;3;5\right\}\\ X=\left\{1;2;3;4\right\}\\ X=\left\{1;2;3;5\right\}\\ X=\left\{1;3;4;5\right\}\\ X=\left\{1;2;3;4;5\right\}\)
\(\left\{1;2;a\right\};\left\{1;2;a;b\right\};\left\{1;2;a;x\right\};\left\{1;2;a;y\right\};\left\{1;2;a;b;x\right\};\left\{1;2;a;b;y\right\};\left\{1;2;a;x;y\right\};\left\{1;2;a;b;x;y\right\}\)
Vậy có 8 tập hợp X
Mk nghĩ là như thê này
Câu 1:
6 chia hết cho x-1 => x-1 là ước của 6.Mà Ư(6)={1;-1;2;-2;3;-3;6;-6}=> x={2;0;3;-1;4;-2;7;-5}
Câu 2;
14 chia hết cho 2x+3
=>2x+3 là ước của 14.Mà Ư(14)={1;-1;2;-2;7;-7;14;-14}
=>x={-1;-2;2;-5;}
Chọn C
+ Gọi số cần tìm là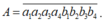
Ta có tổng các chữ số của A là 1 + 2 + 3 + 4 + .... + 8 = 36 chia hết cho 9 nên A chia hết cho 9.
Do 9 và 111 có ƯCLN là nên A chia hết cho 9999.
Đặt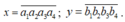
Ta có:
Mà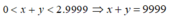
+ Từ tập X có 4 cặp số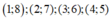
nên có: 8 cách chọn
a
1
; 6 cách chọn
a
2
; 4 cách chọn
a
3
và 2 cách chọn
a
4
.
Vì a i và b i tạo thành một cặp để a i + b i = 9 nên chọn a i có luôn b i .
=> Số các số cần tìm là: 8.6.4.2 = 384 số
Vậy xác suất cần tìm là: