Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
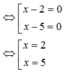
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
cho tập hợp A = { -3 ;-2 ; 0 ; 6 ; 9 }. trong các 1 tập hợp sau tập hợp nào ko phải là tập hợp con của A ?
A. {-3 , 9} B. {-2 , 0 , -9 } C. {-3 ,0 , 6 ,9 } D . {-2}
Tập hợp C rỗng vì \(x^2+7x+12=0\Leftrightarrow x\in\left\{-3;-4\right\}\notin N\)
\(a,\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\}\\ b,\left\{1\right\};\left\{2\right\};\left\{3\right\};\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\};\left\{1;2;3\right\}\)
\(X=\left\{1;3\right\}\\ X=\left\{1;2;3\right\}\\ X=\left\{1;3;4\right\}\\ X=\left\{1;3;5\right\}\\ X=\left\{1;2;3;4\right\}\\ X=\left\{1;2;3;5\right\}\\ X=\left\{1;3;4;5\right\}\\ X=\left\{1;2;3;4;5\right\}\)
Đáp án D
Phương pháp: Xét từng trường hợp: chữ số đầu tiên bằng 1, chữ số thứ hai bằng 1, chữ số thứ ba bằng 1.
Cách giải: Gọi số đó là a b c d e
- TH1: a = 1
+ b có 7 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 7.6.5.4 = 840 số
- TH2: b = 1
+ a ≠ b , a ≠ 0 , nên có 6 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 6.6.5.4 = 720 số.
- TH3: c = 1.
+ a ≠ c , a ≠ 0 , nên có 6 cách chọn.
+ b có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có 6.6.5.4 = 720 số.
Vậy có tất cả 840 + 720 + 720 = 2280 số.