Cho một con lắc lò xo treo thẳng đứng. Một học sinh tiến hành hai lần kích thích dao động. Lần thứ nhất, nâng vật lên rồi thả nhẹ thì thời gian ngắn nhất vật đến vị trí lực đàn hồi triệt tiêu là
∆
t
1
. Lần thứ hai, đưa vật về vị trí lò xo không biến dạng rồi thả nhẹ thì thời gian ngắn nhất đến lúc lực phục hồi đổi chiều là
∆
t
2
Tỉ...
Đọc tiếp
Cho một con lắc lò xo treo thẳng đứng. Một học sinh tiến hành hai lần kích thích dao động. Lần thứ nhất, nâng vật lên rồi thả nhẹ thì thời gian ngắn nhất vật đến vị trí lực đàn hồi triệt tiêu là ∆ t 1 . Lần thứ hai, đưa vật về vị trí lò xo không biến dạng rồi thả nhẹ thì thời gian ngắn nhất đến lúc lực phục hồi đổi chiều là ∆ t 2 Tỉ số ∆ t 1 ∆ t 2 = 2 3 . Tỉ số gia tốc vật và gia tốc trọng trường ngay khi thả lần thứ nhất là
A. 0,8.
B. 1,5.
C. 12.
D. 2.
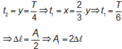
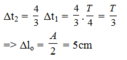
Đáp án D.
Lực phục hồi đổi chiều tại VTCB. Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
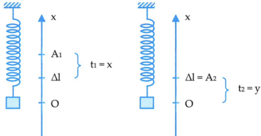
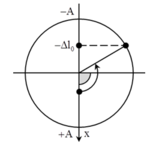
Lần thứ hai: khi đưa vật về vị trí lò xo không biến dạng rồi thả nhẹ thì quãng đường vật chuyển động đến lúc lực phục hồi đổi chiều (VTCB) bằng A, tương ứng với thời gian vật chuyển động bằng T/4
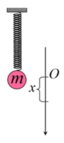
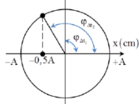
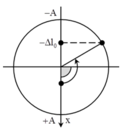
Lần thứ nhất: khi nâng vật lên rồi thả nhẹ vật chuyển động trên vị trí lực đàn hồi triệt tiêu tức là vật đã chuyển động từ vị trí biên (có ly độ x = -A) đến vị trí có ly độ x = - ∆ l 0 (chọn chiều dương Ox hướng xuống)
Do thời gian
Vậy tỉ số gia tốc vật và gia tốc trọng trường ngay khi thả lần thứ nhất là