Cho nửa đường tròn (O), đường kính AB. Trên một nửa mặt phẳng bờ AB có chứa nửa
đường tròn, vẽ các tia tiếp tuyến Ax, By với đường tròn (O). Gọi H là một điểm bất kỳ
trên nửa đường tròn (H không trùng A và B). Tiếp tuyến của đường tròn tại H lần lượt
cắt Ax và By tại C và D.
a) Chứng minh AC + BD = CD
b) Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp tam giác COD.
c) Tìm vị trí của điểm H trên nửa đường tròn sao cho diện tích tứ giác
ACDB nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
góc DMO+góc DBO=180 độ
=>DMOB nội tiếp
b: Xét (O) có
CM,CA là tiếp tuyến
=>CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc DOC=1/2*180=90 độ
Xét ΔDOC vuông tại O có OM là đường cao
nên CM*MD=OM^2
=>AC*BD=R^2

a: Xét (O) có
MA,MH là tiếp tuyến
nên MA=MH
mà OA=OH
nên OM là phân giác của góc AOH(1) và HM=MA
Xét (O) có
NH,NB là tiếp tuyến
nên NH=NB và ON là phân giác của góc HOB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
AM*BN=HM*HN=OH^2=R^2
b: AM+BN=HN+HM>=2*OH=AB
Dấu = xảy ra khi MN=AB
=>H trùng với O

a:góc ABD=góc DCA
góc ABD=góc FAD(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AD)
góc FAD=góc CAD
=>góc ABD=góc CBD
=>BD là phân giác của góc ABE
mà góc ADB=90 độ
nên BD là đường cao
=>ΔBAE cân tại B
b: Xét ΔEAB có
AC,BD là các đường cao
AC cắt BD tại K
Do đó: K là trực tâm
=>EK vuông góc với BA
c: Xét ΔAKF có AD vừa là đường cao, vừa là phân giác
nên ΔAKF cân tại A
=>góc AKF=góc AFK=góc KFE
=>AK//FE
Xét tứ giác AKEF có
AK//FE
AF//KE
KE=KA
Do đó: AKEF là hình thoi

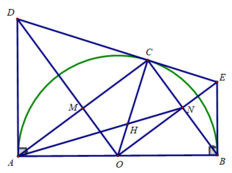
d) Ta có: N là trung điểm của BC
⇒ AN là trung tuyến của ΔABC
CO cũng là trung tuyến của ΔABC
AN ∩ CO = H
⇒ H là trọng tâm ΔABC
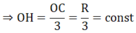
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn
(O; R/3)

b: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: MN=MC+NC
nên MN=MA+NB

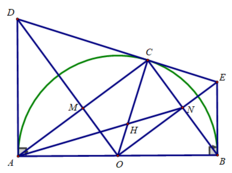
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE

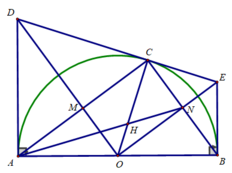
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC 2 = R 2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC 2 = R 2
Khi đó: OM.OD + ON.OE = 2 R 2
Vậy OM.OD + ON.OE không đổi
a, Theo tính chất 2 tt cắt nhau: \(AC=CH;BD=DH\Rightarrow AC+BH=CH+HD=CD\)
b, Vì \(AC=CH;CO.chung;\widehat{CAO}=\widehat{CHO}=90^0\) nên \(\Delta CAO=\Delta CHO\left(cgv-ch\right)\)
Do đó \(\widehat{AOC}=\widehat{COH}\) hay OC là p/g \(\widehat{AOH}\)
Tương tự: \(\widehat{BOD}=\widehat{DOH}\) hay OD là p/g \(\widehat{HOB}\)
\(\Rightarrow\widehat{COD}=\widehat{COH}+\widehat{HOD}=\dfrac{1}{2}\left(\widehat{AOH}+\widehat{HOB}\right)=90^0\\ \Rightarrow\Delta OCD\perp O\)
Do đó OCD nội tiếp đường tròn tâm là trung điểm CD
Gọi I là trung điểm CD
Xét hthang ABDC(AC//BD) có O là trung điểm AB, I là trung điểm CD nên OI là đtb ht ABDC
\(\Rightarrow OI//AC\\ \Rightarrow OI\perp AB\)
Vậy AB là tt đường tròn nt tg OCD