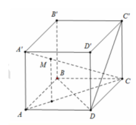
Cho hình lập phương ABCD.A’B’C’D’. Gọi M là điểm trên đường chéo CA’ sao cho ![]() Tính tỉ số giữa thể tích
V
1
của khối chóp M.ABCD và thể tích
V
2
của khối lập phương
Tính tỉ số giữa thể tích
V
1
của khối chóp M.ABCD và thể tích
V
2
của khối lập phương
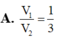
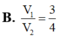
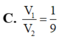
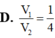
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
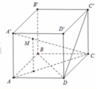
Do M C A ' C = 3 4 ⇒ d N ; A B C d M ; A B C = 3 4
Ta có
V M . A B C D = 1 3 S A B C D . d M ; A B C D = 1 3 S A B C D . 3 4 d A ; A B C D = 1 4 V A B C D . A ' B ' C ' D ' ⇒ V 1 V 2 = 1 4

Đáp án D
Ta có V 1 = 1 3 . 3 a 4 . a 2 = a 3 4 ; V 2 = a 3 ⇒ V 1 V 2 = 1 4 .

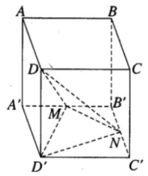
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
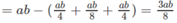
Thể tích khối chóp
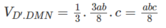
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8

Tương tự 2A.
a) Hình chóp S.MNPQ là hình chóp đều vì các mặt bên là tam giác cân và đáy MNPQ là đa giác đều.
b)
V
'
V
=
1
6
. Chú ý 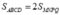

Chọn B
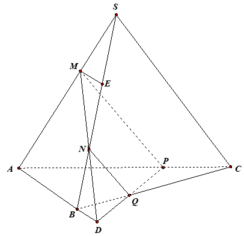
Trong mặt phẳng (SAC) dựng MP song song với SC cắt AC tại P. Trong mặt phẳng (SBC) dựng NQ song song với SC cắt BC tại Q. Gọi D là giao điểm của MN và PQ. Dựng ME song song với AB cắt SB tại E (như hình vẽ).
Ta thấy: ![]()
Suy ra N là trung điểm của BE và DM, đồng thời
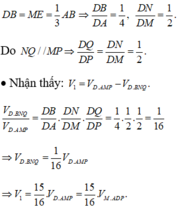
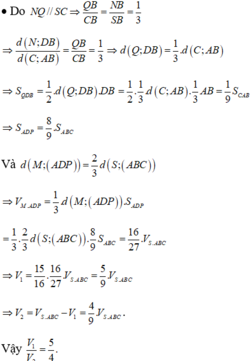

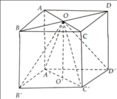
a) Bốn tam giác OAA', OBB', OCC', ODD' là các tam giác vuông bằng nhau nên suy ra OA' = OB' = OC' = OD'.
Hình chóp O.A'B'C'D' là hình chóp đều vì có các mặt bên là tam giác cân và đáy là đa giác đều.
b) Thể tích của của hình chóp O.A'B'C'D' là:
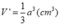
Thể tích hình lập phương:
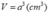
Vậy V ' V = 1 3