Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, AC =a 3 và BB'C'C là hình vuông. Khoảng cách giữa hai đường thẳng AA' và BC' là
A. a 3 2
B. 3 a 2 4
C. a
D. a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

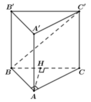
Gọi H là hình chiếu của A lên BC
Ta có 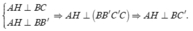
Suy ra AH là đoạn vuông góc chung của AA' và BC' nên
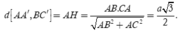
Chọn C.

nhận thấy\(AA^,\) //mp(\(BB^,C^,C\)) mà \(BC^,\) thuộc mp(\(BB^,C^,C\)) nên khoảng cách " d" giữa hai đương thẳng là khoảng cách giữa đt \(AA^,\) và mp( \(BB^,C^,C\))
trong mp(ABC) từ A kẻ AH vuông góc BC cắt tại H ,mà AH \(\perp\)B\(B^,\) suy ra AH \(\perp\) mp\(BB^,C^,C\)
ta có d=AH \(=\sqrt{1:\left(\frac{1}{AB^2}+\frac{1}{AC^2}\right)}=\frac{a\sqrt{3}}{2}\)

Đáp án B
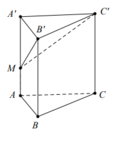
Ta có B C / / B ' C ' ⇒ B C / / M B ' C ' ⇒ d B C ; C ' M = d B ; M B ' C ' = d = 3 V B . M B ' C ' S M B ' C '
Lại có V B . M B ' C ' = V M . B B ' C ' = V A ' . B B ' C ' = 1 3 B B ' . S A ' B ' C ' = 4 a 3 3 .
Ta có M B ' = A ' B ' 2 + A ' M 2 = a 13 M C ' = A ' C ' 2 + A ' M 2 = a 10 B ' C ' = A ' B ' 2 + A ' C ' 2 = a 5
Sử dụng công thức Heron S = p p - a p - b p - c . Trong đó a,b,c là độ dài ba cạnh của một tam giác và p = a + b + c 2 . Ta được S M B ' C ' = 7 a 2 2 ⇒ d = 3 . 4 a 3 3 7 a 2 2 = 8 a 7 .

Đáp án A
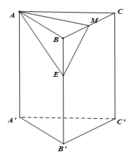
Gọi E là trung điểm của BB' => ME//B'C => (AME)//B'C
![]() = d(C;(AME))
= d(C;(AME))
Vì ![]()
![]()
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên :
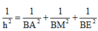
![]()
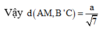
Chọn A.
Gọi H là hình chiếu của A lên BC. Ta có
Suy ra AH là đoạn vuông góc chung của AA' và BC' nên