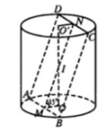
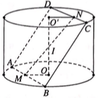
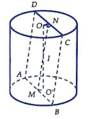
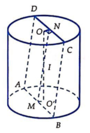
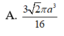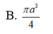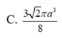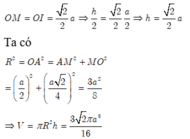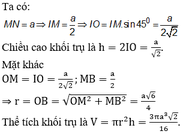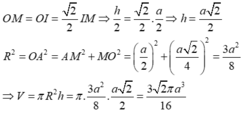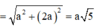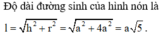Cho một hình trụ tròn xoay và hình vuông (ABCD) cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc . Thể tích của hình trụ bằng