Cho tứ diện S.ABC trên đoạn thẳng SA, SB, SC lần lượt lấy các điểm M, N, P sao cho SM=5MA SN=2NB và SP=kPC Kí hiệu
V
T
là thể tích của khối đa diện T. Biết rằng 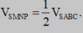 Tìm k?
Tìm k?

![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

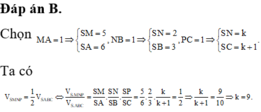

Đáp án B.
Chọn M A = 1 ⇒ S M = 5 S A = 6 , N B = 1 ⇒ S N = 2 S B = 3 , P C = 1 ⇒ S N = k S C = k + 1 .
Ta có V S M N P = 1 2 V S A B C ⇔ V S . M N P V S . A B C = S M S A . S N S B . S P S C = 5 6 . 2 3 . k k + 1 = 1 2 ⇒ k k + 1 = 9 10 ⇒ k = 9 .

Chọn D.
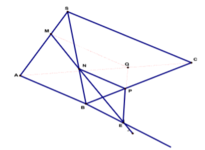
Mp ( α ) qua MN và song song với SC. Mp ( α ) cắt BC và cắt AC tại P và Q ta có:
NP // SC nên ![]() Ta có: MN, PQ, AB đồng quy tại E.
Ta có: MN, PQ, AB đồng quy tại E.
Áp dụng định lí Mennelauyt trong tam giác SAB, ta có:
![]()
![]()
Áp dụng định lí Menelauyt trong tam giác ABC ta có: ![]()
![]()
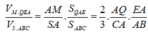
![]()
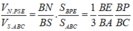
![]()
![]()
![]()
![]()
Vậy 

Đáp án A
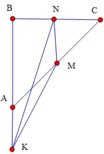
Gọi H là hình chiếu của S lên mặt đáy A B C suy ra S H ⊥ A B C thì H là trung điểm của AC.
Ta có:
S H = 9 − 2 = 7 ; K = P Q ∩ A B ; A B = A C = 2
Dựng P E / / A B ta có:
K B P E = Q B Q E = 1 ⇒ K B = P E = 1 3 A B = 2 3
S M N K = 1 2 d K ; M N . M N = 1 2 N B . M N = 1 2 d P ; A B C = 2 3 . S H = 2 3 7 ⇒ V P . M N K = 1 3 d P ; A B C . S M N K = 7 9
Lại có:
K Q K P = 1 2 ⇒ V Q . M N P V K . M N P = 1 2 ⇒ V Q . M N P = 1 2 V K . M N P = 7 18
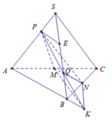

Đáp án là B
Theo công thức tỉ số thể tích của hình chóp tam giác ta có
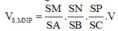
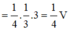

Đáp án C
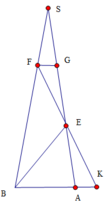
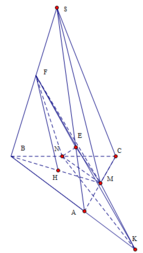
Ta có ∆ A B C vuông cân tại B nên M là tâm đường tròn ngoại tiếp. S M = S B = S C ⇒ S M ⊥ ( A B C )
F E ∩ A B = K , kẻ F G / / B A F H / / S M ⇒ F H ⊥ ( A B C ) ta có: F H = 2 3 S M = 2 3 S A 2 - A M 2 = 2 3 12 2 - 8 = 4 3 34
d t K M N = d t B N M K - d t B N K = 1 2 ( M N + B K ) . B N - 1 2 M N . B N = 1 2 . 2 . 2 = 2
∆ F G E = ∆ K A E ( C . G . C ) ⇒ F E = 1 2 F K
V F M N E V F M N K = F E F K = 1 2 ⇒ V F M N E = 1 2 V F M N K = 1 2 . 1 3 . F H . d t K M N = 1 6 . 4 3 34 . 2 = 4 34 9