Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SA và BC. Biết góc giữa MN và mặt phẳng (ABCD) bằng 60 0 . Khoảng cách giữa hai đường thẳng BC và DM là:
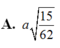
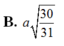
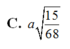
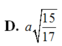
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có M N , A B C D = ^ M N H ^ = 60 0 , N H = 3 a 4 2 + a 4 2 = a 10 4 ⇒ M H = a 30 4 ⇒ S O = a 30 2
Gọi I là trung điểm của AD
Kẻ O K ⊥ S I ⇒ d B C , D M = d B C , S A D = d C , S A D = 2 d M , S A D = 2 O K .
Ta có 1 O K 2 = 1 O I 2 + 1 O S 2 = 1 a 2 2 + 1 a 30 2 2 = 124 30 a 2 ⇒ O K = a 30 2 31 .
Vậy d B C , D M = 2 O K = a 30 31 .

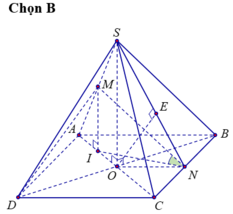
Gọi I là trung điểm OA. Vì IM// SO ⇒ IM⊥(ABCD) nên hình chiếu của MN lên (ABCD) là IN. Suy ra ![]()
Áp dụng định lí cô sin trong ΔCIN, ta có:
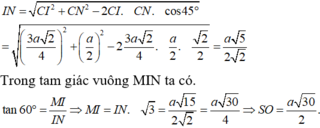
Ta có d(BC, DM) = d(BC, (SAD)) = d(N, (SAD)) = 2d(O, (SAD)) = 2d(O, (SBC)).
Kẻ OE ⊥ SN ⇒ OE ⊥ (SBC).
Ta có d(O, (SBC)) = OE mà
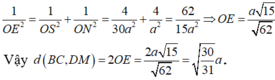

Chọn B
Gọi I là hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó
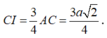
Xét tam giác CNI có
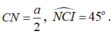
Áp dụng định lý cosin ta có:
![]()

Xét tam giác MIN vuông tại I nên
![]()
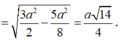
Mà MI//SO
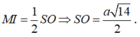
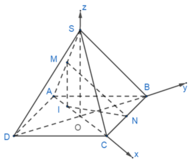
Chọn hệ trục tọa độ như hình vẽ. Ta có:
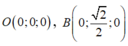
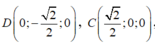
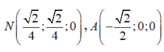
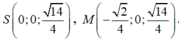
Khi đó
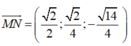
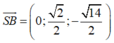
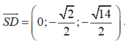
Vectơ pháp tuyến mặt phẳng (SBD)
![]()
Suy ra
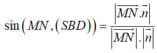
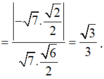
Đáp án B
dạ cho em hỏi là tại sao tính NH như vậy được ạ ?? Em cảm ơn!!