Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp:
- Coi hai ông Trum và Kim là một người thì bài toán trở thành xếp 9 người vào dãy ghế.
- Lại có 2 cách đổi chỗ hai ông Trum và Kim nên từ đó suy ra đáp số.
Cách giải:
Kí hiệu 10 vị nguyên thủ là a, b, c, d, e, f, g, h, i, k.
Và hai ông Trum, Kim lần lượt là a, b.
Nếu ông Trum ngồi lên bên trái ông Kim, tương đương xếp a b ¯ , c , d , e , f , g , h , i , k vào 9 vị trí. Ta có A 9 9 cách.
Vậy tổng hợp lại, có A 9 9 + A 9 9 = 2.9 ! cách.
- Đếm số cách để A và B ngồi cạnh nhau, C ngồi vị trí bất kì:
Coi A, B là một người, có \(2!\) cách xếp vị trí A, B.
Khi đó ta xếp vị trí của 9 người: \(9!\).
Có tổng số cách xếp là: \(2!.9!\).
- Đếm số cách để A và B ngồi cạnh nhau, C ngồi cạnh A.
Coi A, B, C là một người. Có 2 cách xếp thỏa mãn là CAB, BAC.
Khi đó ta xếp vị trí của \(8\) người: \(8!\).
Có số cách xếp là: \(2.8!\).
Vậy số cách xếp để A và B ngồi cạnh nhau, A và C không ngồi cạnh nhau là \(2!.9!-2.8!\).
a) Có 2. 9 = 18 cách xếp chỗ cho An và Bình ngồi cạnh nhau.
8 bạn kia được xếp vào 8 chỗ còn lại. Vậy có 8! cách xếp 8 bạn còn lại và do đó có 18! 8 cách xếp sao cho An, Bình ngồi cạnh nhau.
b) Có 10! cách xếp chỗ ngồi cho 10 bạn.
Từ đó có 10! - 18. 8! = 72. 8! cách xếp chỗ cho 10 bạn mà An và Bình không ngồi cạnh nhau.
a) Xếp hai người đàn bà ngồi cạnh nhau.Có 2 cách.
Sau đó xếp đứa trẻ ngồi vào giữa. Có 1 cách.
Xếp 4 người đàn ông vào 4 ghế còn lại. Có 4! cách.
Theo quy tắc nhân, có 2. 4! = 48 cách.
b) Đầu tiên chọn 2 người đàn ông. Có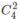 
cách.
Xếp hai người đó ngồi cạnh nhau. Có 2 cách.
Sau đó xếp đứa trẻ vào giữa. Có 1 cách.
Xếp 4 người còn lại vào 4 ghế còn lại. Có 4! cách.
Vậy theo quy tắc nhân, có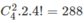 
cách.
Đáp án A
Phương pháp:
- Coi hai ông Trum và Kim là một người thì bài toán trở thành xếp 9 người vào dãy ghế.
- Lại có 2 cách đổi chỗ hai ông Trum và Kim nên từ đó suy ra đáp số.
Cách giải:
Kí hiệu 10 vị nguyên thủ là a, b, c, d, e, f, g, h, i, k.
Và hai ông Trum, Kim lần lượt là a, b.
Nếu ông Trum ngồi lên bên trái ông Kim, tương đương xếp a b , c, d, e, f , g, h ,i ,k vào 9 vị trí. Ta có A 9 9 cách.
Vậy tổng hợp lại, có A 9 9 + A 9 9 = 2 . 9 ! cách.