Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB = 2a,BC = a. Các cạnh bên của hình chóp bằn nhau và bằng
a
2
. Gọi E và F lần lượt là trung điểm của AB và CD, K là điểm bất kỳ tên AD. Khoảng cách giữa hai đường thẳng EF và SK là? A.
a
3
3
. B.
a
6
3
. C.
a
15
5
. D.
a
21
...
Đọc tiếp
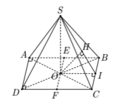
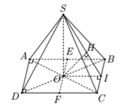
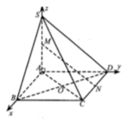
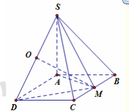
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB = 2a,BC = a. Các cạnh bên của hình chóp bằn nhau và bằng a 2 . Gọi E và F lần lượt là trung điểm của AB và CD, K là điểm bất kỳ tên AD. Khoảng cách giữa hai đường thẳng EF và SK là?
A. a 3 3 .
B. a 6 3 .
C. a 15 5 .
D. a 21 7 .
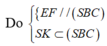
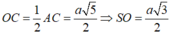
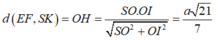
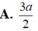
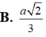
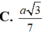
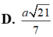
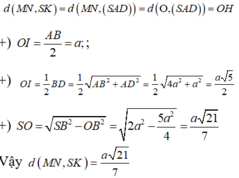
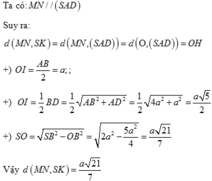
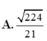
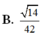
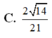
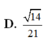
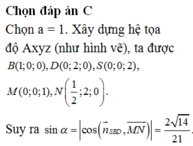
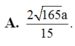
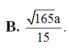
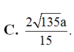
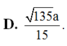
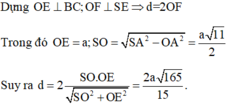
Đáp án: D.
Hướng dẫn giải:
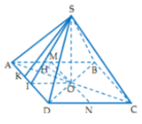
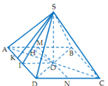
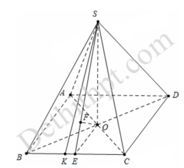
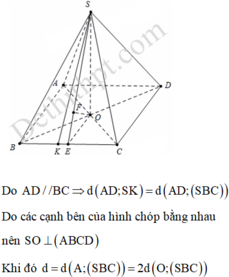
O = A C ∩ B D , Gọi , I là trung điểm cạnh đáy BC.
Vì SA = SB = SC = SD nên S O ⊥ ( A B C D )
Từ đó ta chứng mình được B C ⊥ ( S O I )
⇒ O H ⊥ ( S B C ) (với O H ⊥ B C tại SI).
Do E F / / ( S B C ) S K ⊂ ( S B C )
nên d(EF,SK) = d(EF,(SBC)) = OH.
Thực hiện tính toàn để được
O C = 1 2 A C = a 5 2 ⇒ S O = a 3 2
Kết luận: