tìm n lớn nhất : (2n+12) chia hết (n-1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có \(\frac{2n+12}{n+2}=\frac{2\left(n+2\right)+8}{n+2}=2+\frac{8}{n+2}\)
\(\Rightarrow n+2\in\left\{B\left(8\right)\text{/n}+2\le8\right\}\)
\(\Rightarrow\)n+2 lớn nhất là 8
vậy n=6

\(\left(\frac{2n+1}{n-3}=2+\frac{7}{n-3}=>n=\left\{4,10\right\}\right)\)
\(\frac{n^2+3}{n+1}=\frac{n^2-1+4}{n+1}=\left(n-1\right)+\frac{4}{n+1}=>n=\left\{0,1,3\right\}\)
\(n=2^a.3^b=>2^5.3=96\)
\(n=2^a=2^6=64\)
\(n=2^a.3^b=2^3.3^2=8.9=72\)

= ( 2n + 2 ) + 10 chia hết cho n + 1
Mà 2n chia hết cho n + 1
= 10 chia hết cho n + 1
= n + 1 thuộc U( 10)=(1;2;5;10)
= n thuộc (0;1;4;9)
Mà n là số tự nhiên lớn nhất
= n =9
(2n + 12) \(⋮\)(n-1)
(2n - 2 + 14) \(⋮\)(n - 1)
2 (n - 1) + 14 \(⋮\)(n - 1)
2 (n -1) \(⋮\)(n - 1)
14 \(⋮\)(n - 1 ) => (n - 1) \(\in\)Ư(14) = {2; 7}
| n - 1 | 2 | 7 |
| n | 3 | 8 |

Ta có : 2n+12 = 2n - 2 + 14 = 2(n-1) + 14.Vì 2(n-1) chia hết cho n-1 nên để 2n+12 chia hết cho n-1 thì 14 chia hết cho n-1 mà n lớn nhất nên n-1 lớn nhất => n-1 = 14 => n =15
Vậy số tự nhiên n lớn nhất thỏa mãn 2n+12 chia hết cho n-1 là 15.


2n+12 chc n-1
2n-2+14 chc n-1
14 chc n-1
n-1 thuộc Ư(14)={1;2;7;14}
Đến đây bạn tự làm đc chú ý n lớn nhất đấy nhé

=>(2n+2)+10 chia hết cho n+1
=>2(n+1)+10 chia hết cho n+1
Mà 2(n+1) chia hết cho n+1
=>10 chia hết cho n+1
=>n+1 thuộc Ư(10)={1;2;5;10}
=>n thuộc {0;1;4;9}
Mà n là số tự nhiên lớn nhất
=>n=9
2(n+1)+4 chia het n+1
4 chia het cho n+1
n+1 E {1;2;4}
nE{0;1;3}
de n lon nhat suy ra n=3
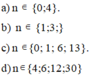
n = 15