Hình bên là đồ thị của hàm số y = x 3 - 3 x . Tìm tất cả các giá trị thực của tham số m để phương trình 64 x 3 = x 2 + 1 2 12 x + m x 2 + 1 có nghiệm.
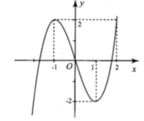
A. - 2 ≤ m ≤ 2
B. Với mọi m
C. m ≥ 0
D. m ≥ - 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()

Đáp án D
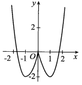
Từ đồ thị hàm số đã cho (như hình vẽ) ta suy ra đồ thị của hàm số
![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán
: ![]()

Chọn D.
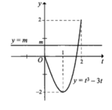
Để phương trình f(x)=m+2 có 4 nghiệm phân biệt thì đường thẳng y=m+2 phải cắt đồ thị hàm số y=f(x) tại 4 điểm phân biệt.
Dựa vào đồ thị ta được -4<m+2<-3 => -6<m<-5

Đáp án D
Từ đồ thị đã cho ta suy ra đồ thị hàm số ![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán là ![]()

Đáp án A
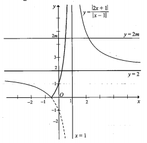
Dựa vào đồ thị hàm số y = f x , để phương trình f x = m có 2 nghiệm phân biệt ⇔ m > 5 0 < m < 1

+ Trước tiên từ đồ thị hàm số y= f( x) , ta suy ra đồ thị hàm số y = |f(x)| như hình dưới đây:

Phương trình 2|f(x)| - m = 0 hay |f(x)| = m/2 là phương trình hoành độ giao điểm của đồ thị hàm số y = |f(x) và đường thẳng y= m/2.
Dựa vào đồ thị hàm số y = |f(x)|, ta có ycbt trở thành:
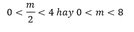
Chọn A.
Chọn A