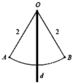
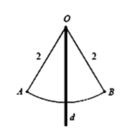
Gọi (H) là khối tròn xoay tạo thành khi quay hình quạt OAB (hình vẽ bên) quanh đường thẳng d đi qua O và vuông góc với AB. Biết O A = O B = 2 , góc A O B = 60 ° . Thể tích V của khối tròn xoay H gần với giá trị nào sau đây nhất ?
A. 1,75
B. 2,25
C. 1,55
D. 3,15





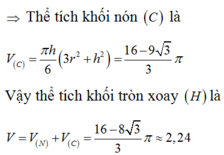

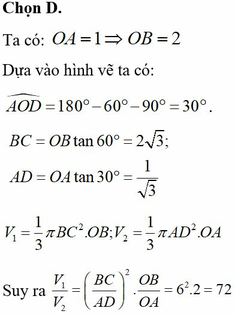
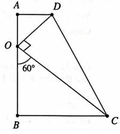

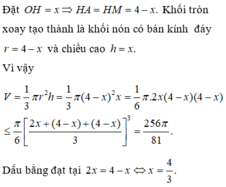
Đáp án B
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24
Đáp án B
Giari thích các bước :
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24