Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
"sao không cho đủ 3 màu" nghĩa là gì bạn? Đủ 3 màu hay không đủ 3 màu?
Chắc là "Sao cho không đủ ba màu"
Nếu em làm là trước hết tìm số cách chọn 4 viên bất kì, sau đó tìm số cách chọn 4 viên có đủ ba màu, sau em lấy cái 4 viên bất kì trừ đi số viên có đủ 3 màu.
Nhưng mà không biết em sai ở đâu chỗ tìm 4 viên có đủ ba màu.
Đoạn này em làm là:
Số cách chọn 4 viên bất kì là: \(C_{15}^4=1365\) cách
Có \(4.5.6\) cách chọn 3 viên ba màu khác nhau, sau đó chọn thêm 1 viên bất kì từ 12 viên còn lại. Sau cùng được \(4.5.6.12=1440\) (vô lí)
Chỉ ra lỗi sai giúp em với ạ.
+ Loại 1: chọn tùy ý trong 15 viên bi có C 15 4 = 1365 cách
+ Loại 2: chọn đủ cả 3 màu có 720 cách gồm các trường hợp sau:
- Chọn 2 bi đỏ, 1 bi trắng và 1 bi vàng có 180 cách
- Chọn 1 bi đỏ, 2 bi trắng và 1 bi vàng có 240 cách
- Chọn 1 bi đỏ, 1 bi trắng và 2 bi vàng có 300 cách
Vậy có 1365 - 720 = 645 cách
Đáp án D
TH1: 4 viên được lấy chỉ gồm 2 màu đỏ và trắng.
\(\Rightarrow\) Có \(C^4_7\) cách chọn.
TH2: 4 viên được lấy chỉ gồm 2 màu đỏ và vàng.
\(\Rightarrow\) Có \(C^4_8\) cách chọn.
TH3: 4 viên được lấy chỉ gồm 2 màu trắng và vàng.
\(\Rightarrow\) Có \(C^4_9\) cách chọn.
TH2 và TH3 đã bao gồm TH lấy 4 viên chỉ có màu trắng và 4 viên chỉ có màu vàng.
\(\Rightarrow\) Có \(C^4_7+C^4_8+C^4_9-C^4_4-C^4_5=225\) cách chọn ra 4 viên bi không đủ ba màu.
a.
Có \(C_{17}^5\) cách lấy 5 viên bi tùy ý từ 17 viên bi
b.
Lấy 1 bi trắng từ 7 bi trắng, 2 bi xanh từ 4 bi xanh và 2 bi đỏ từ 6 bi đỏ
Số cách lấy là: \(C_7^1.C_4^2.C_6^2\) cách
c.
Các trường hợp thỏa mãn: 1 trắng 1 đỏ 3 xanh, 1 trắng 2 đỏ 2 xanh, 1 trắng 3 đỏ 1 xanh, 2 trắng 1 đỏ 2 xanh, 2 trắng 2 đỏ 1 xanh
Số cách lấy là:
\(C_7^1C_6^1C_4^3+C_7^1C_6^2C_4^2+C_7^1C_6^3C_4^1+C_7^2C_6^1C_4^2+C_7^2C_6^2C_4^1\) cách
Thầy có thể giải thích cụ thể hơn về câu a được không thưa thầy?
Đáp án D
+ Trường hợp 1: chọn 4 bi đỏ hoặc trắng có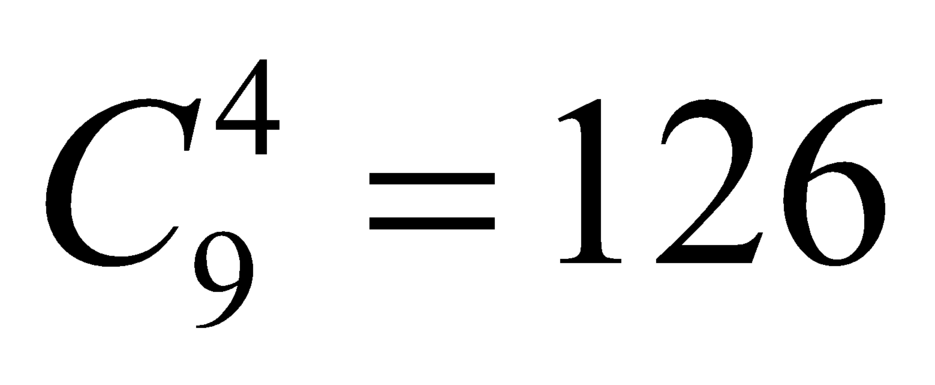
cách
+ Trường hợp 2: chọn 4 bi đỏ và vàng hoặc 4 bi vàng có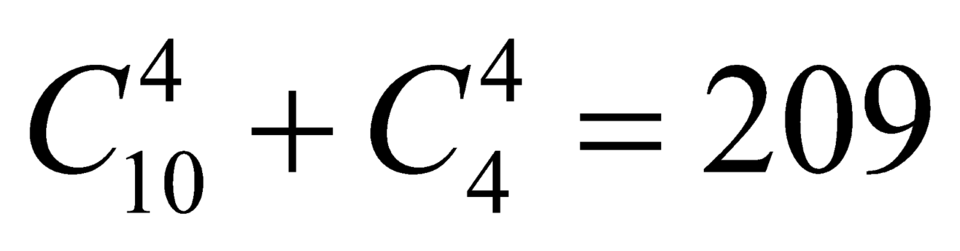
cách
+ Trường hợp 3: chọn 3 bi trắng và vàng có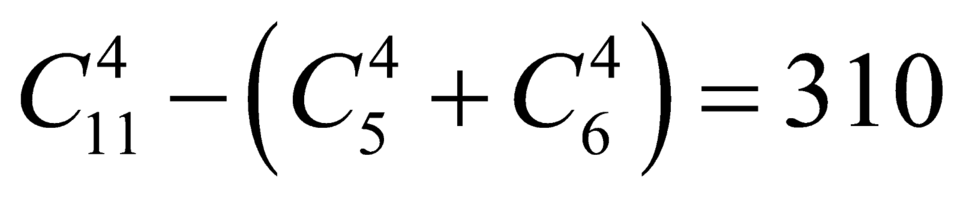
cách
Vậy có
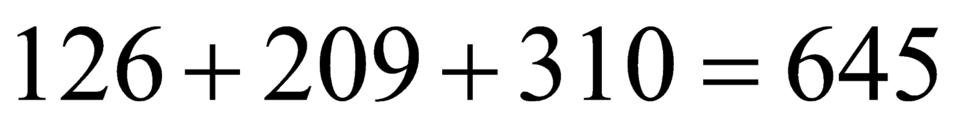cách
D