Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác AMBN có
Q là trung điểm của AB
Q là trung điểm của MN
Do đó: AMBN là hình bình hành
mà MA=MB
nên AMBN là hình thoi
Chọn đáp án C.
Chuẩn hóa BC = 5; AC = 4; AB = 3 →∆ABC vuông tại A.
Khi quay ∆ABC quanh AC, ta được khối nón N 1 có bán kính đáy r = AB = 3, độ dài đường sinh l = BC = 5 suy ra diện tích toàn phần của N 1 là S b = 24 π
Khi quay ∆ABC quanh AB, ta được khối nón N 2 có bán kính đáy r = AC = 4, độ dài đường sinh l = BC = 5 suy ra diện tích toàn phần của N 2 là S c = 36 π
Khi quay ∆ABC quanh BC, ta được khối nón N 3 , N 4 có bán kính đáy là chiều cao của tam giác ABC và bằng 12/5, độ dài đường sinh lần lượt là 3,4 suy ra diện tích toàn phần của khối tròn xoay S a = S 3 + S 4 = 708 π 25
Vậy S C > S a > S b
a: Xét ΔCAB có CE/CA=CD/CB
nên ED//AB và ED=AB/2
=>AEDB là hình thang
mà góc EAB=90 độ
nênAEDB là hình thang vuông
b: Xét tứ giác ABKC có
D là trung điểm chung của AK và BC
góc BAC=90 độ
Do đó: ABKC là hình chữ nhật
a. Xét \(\Delta ABC\) có: \(\left\{{}\begin{matrix}CF=BF\\BD=AD\end{matrix}\right.\)\(\Rightarrow\)DF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)DF//AC hay DF//EC(1)
Lại có, xét \(\Delta ABC\): \(\left\{{}\begin{matrix}CE=AE\\BD=AD\end{matrix}\right.\)\(\Rightarrow\) ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) ED//BC hay ED//CF(2)
Từ (1) và (2) suy ra tứ giác FDEC là hình bình hành
b. Ta có: \(\left\{{}\begin{matrix}FD//AC\\AC\perp AB\end{matrix}\right.\) \(\Rightarrow FD\perp AB\Rightarrow\widehat{FDA}=90^o\)
Tương tự xét \(\Delta ABC\) có: \(\left\{{}\begin{matrix}CE=AE\\CF=BF\end{matrix}\right.\)\(\Rightarrow\)EF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) EF//AB
Có: \(\left\{{}\begin{matrix}EF//AB\\AC\perp AB\end{matrix}\right.\)\(\Rightarrow EF\perp AC\Rightarrow\widehat{FEA}=90^o\)
Xét tứ giác EFDA có: \(\widehat{FEA}=\widehat{EFD}=\widehat{EAD}=90^o\)
\(\Rightarrow\) Tứ giác EFDA là hình chữ nhật \(\Rightarrow\) AF=DE
c. Xét \(\Delta AKC\) vuông tại K có KE là đường trung tuyến ứng với cạnh huyền
\(\Rightarrow EK=\dfrac{AC}{2}=CE=EA\)
Mà EA=DF (EDFA là hình chữ nhật)
\(\Rightarrow EK=DF\)
Xét tứ giác KDEF có: \(\left\{{}\begin{matrix}DK//EF\\DF=EK\end{matrix}\right.\)\(\Rightarrow\) Tứ giác KDEF là hình thang cân
a) Xét ΔABC có
F là trung điểm của AC(gt)
M là trung điểm của BC(gt)
Do đó: FM là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒FM//AB và \(FM=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà E∈AB và \(AE=\dfrac{AB}{2}\)(E là trung điểm của AB)
nên FM//AE và FM=AE
Xét tứ giác AEMF có
FM//AE(cmt)
FM=AE(cmt)
Do đó: AEMF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AEMF có \(\widehat{FAE}=90^0\)(ΔABC vuông tại A)
nên AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
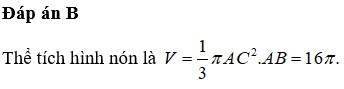
Đáp án B
Thể tích hình nón là V = 1 3 πAC 2 . AB = 16 π