Cho hình chóp S.ABCD. M,N là hai điểm trên AB, CD. Mặt phẳng ( α ) qua MN // SA. Điều kiện của MN để thiết diện của hình chóp ( α ) với là hình thang là
A. MN // AD
B. MN // BC
C. MN là trung điểm AB, CD
D. MN qua trung điểm AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

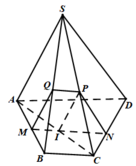
+ Ta tìm thiết diện của hình chóp cắt bởi (α):
Trong ( SAB) dựng MQ // SA( Q thuộc SB)
Gọi I là giao điểm của AC và MN.
Trong mp ( SAC); dựng IP// SA với P thuộc SC.
Khi dó thiết diện cần tìm là tứ giác MNPQ.
+ Tứ giác MNPQ là một hình thang khi MN// PQ hoặc MQ// PN.

=> MN//PQ nên tứ giác MNPQ là hình thang.
Vậy để tứ giác MNPQ là hình thang thì điều kiện là MN//BC.
Chọn C

Đáp án A.
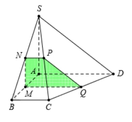
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .

Gọi (α) là mặt phẳng qua O song song với AB và SC.
AB // (α) nên (α) cắt mp(ABCD) theo giao tuyến qua O và song song với AB. Gọi M, N lần lượt là giao điểm của đường thẳng qua O song song AB với BC và AD.
Trong mặt phẳng (SAC) kẻ OP // SC (P ϵ AS) (α) cắt mp(SAB) theo giao tuyến PQ // AB (Q ϵ SB)
Thiết diện cần tìm là tứ giác MNPQ.
Tứ giác MNPQ có PQ // MN nên MNPQ là hình thang.
Đáp án B
Thật vậy, giả sử M N / / B C Ta sẽ chứng minh thiết diện là hình thang.
Khi đó, thiết diện là tứ giác J M J N
Do đó, tứ giác J M J N là hình thang (đpcm)