Cho số nguyên dương n thoả mãn lần lượt là số hạng thứ nhất, thứ 5 và thứ 15 của một cấp số cộng. Giá trị của n bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

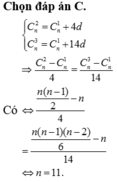

3n+14 =3(n+1) +11 chia hết cho n+1 => 11 chia hết cho n+1
n+1 thuộc U(11) ={1;11}
+ n+1 =1 => n =0 loại
+n+1 =11 => n =10
Vậy n =10

\(\sqrt{3}-\dfrac{m}{n}>0\Leftrightarrow\sqrt{3}>\dfrac{m}{n}\Leftrightarrow3n^2>m^2\)
Vì \(m,n\ge1\) nên \(3n^2\ge m^2+1\)
Với \(3n^2=m^2+1\Leftrightarrow m^2+1⋮3\Leftrightarrow m^2\) chia 3 dư 2 (vô lí)
\(\Leftrightarrow3n^2\ge m^2+2\)
Lại có \(4m^2>1\Leftrightarrow\left(m+\dfrac{1}{2m}\right)^2=m^2+1+\dfrac{1}{4m^2}< m^2+2\)
\(\Leftrightarrow\left(m+\dfrac{1}{2m}\right)^2< 3n^2\Leftrightarrow m+\dfrac{1}{2m}< n\sqrt{3}\\ \Leftrightarrow n\sqrt{3}-m>\dfrac{1}{2m}\)

Lời giải:
Gọi $d=ƯCLN(n+1, 4n^2-2n-5)$
$\Rightarrow n+1\vdots d; 4n^2-2n-5\vdots d$
$\Rightarrow 4(n+1)^2-(4n^2-2n-5)\vdots d$
$\Rightarrow 10n+9\vdots d$
$\Rightarrow 10(n+1)-1\vdots d$
Mà $n+1\vdots d$ nên $1\vdots d\Rightarrow d=1$
Vậy $n+1, 4n^2-2n-5$ nguyên tố cùng nhau. Để $(n+1)(4n^2-2n-5)$ là scp thì bản thân mỗi số $n+1, 4n^2-2n-5$ là scp.
Đặt $n+1=a^2; 4n^2-2n-5=b^2$
$\Rightarrow 4(a^2-1)^2-2(a^2-1)-5=b^2$
$\Leftrightarrow 4a^4-8a^2+4-2a^2+2-5=b^2$
$\Leftrightarrow 4a^4-10a^2+1=b^2$
$\Leftrightarrow 16a^4-40a^2+4=4b^2$
$\Leftrightarrow (4a^2-5)^2-21=4b^2$
$\Leftrightarrow 21=(4a^2-5)^2-(2b)^2=(4a^2-5-2b)(4a^2-5+2b)$
Đến đây là dạng phương trình tích cơ bản, chỉ cần xét các TH để tìm ra $a,b$

đặt 2n + 34 = a^2
34 = a^2-n^2
34=(a-n)(a+n)
a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)
=> a-n 1 2
a+n 34 17
Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ
Vậy ....
Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.
=> S= (1004+14).100:2=50 900 ko là SCP

n+4 là ước của 2n+3 \(\Rightarrow2n+3⋮n+4\)
\(\dfrac{2n+3}{n+4}=\dfrac{2n+8-5}{n+4}=\dfrac{2\left(n+4\right)-5}{n+4}=2-\dfrac{5}{n+4}\)
=> n+4 phải là ước của 5
\(\Rightarrow n+4=\left\{-5;-1;1;5\right\}\Rightarrow n=\left\{-9;-5;-3;1\right\}\)