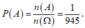Trước kì thi học sinh giỏi, nhà trường tổ chức buổi gặp mặt 10 em học sinh trong đội tuyển. Biết các em đó có số thứ tự trong danh sách lập thành cấp số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế chỉ được ngồi một học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau.
A
.
1
954
...
Đọc tiếp
Trước kì thi học sinh giỏi, nhà trường tổ chức buổi gặp mặt 10 em học sinh trong đội tuyển. Biết các em đó có số thứ tự trong danh sách lập thành cấp số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế chỉ được ngồi một học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau.
A . 1 954
B . 1 126
C . 1 945
D . 1 252
cách
cách
cách
cách
cách
cách
Chọn C.
Giả sử số thứ tự trong danh sách là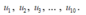
Do dãy này là cấp số cộng nên ta có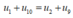
.
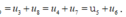Số phần tử của không gian mẫu là n ( Ω ) = 10!
Gọi A là biến cố “Tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau”. Để biến cố này xảy ra ta thực hiện liên tiếp các bước sau:
Bước 1: xếp thứ tự 5 cặp học sinh có các cặp số thứ tự là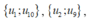
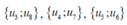vào trước 5 cặp ghế đối diện nhau. Bước này có 5! cách.
Bước 2: xếp từng cặp một ngồi vào cặp ghế đối diện đã ) Chọn ở bước 1. Bước này có 2 5 cách.
Suy ra số kết quả thuận lợi cho biến cố A là 5!. 2 5 .
Vậy xác suất của biến cố A là