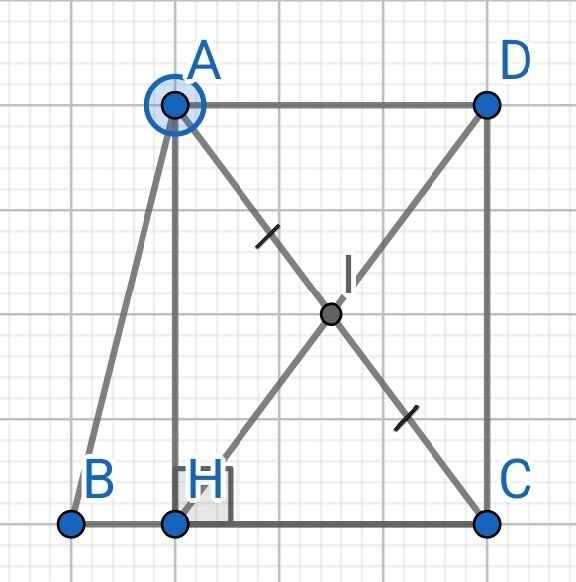
Cho tam giác ABC, đường cao AH, Gọi M là trung điểm của AC Lấy D đối xứng với H qua M. Chứng minh tứ giác AHCD là hình chữ nhật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


 Do D và H đối xứng nhau qua I (gt)
Do D và H đối xứng nhau qua I (gt)
⇒ I là trung điểm của DH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ ∠AHC = 90⁰
Tứ giác AHCD có:
I là trung điểm của AC (gt)
I là trung điểm của DH (cmt)
⇒ AHCD là hình bình hành
Mà ∠AHC = 90⁰ (cmt)
⇒ AHCD là hình chữ nhật

Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
+)Xét tứ giác AHCD có :
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
+)Hình bình hành AHCD có góc AHC = 90độ
=> AHCD là hình chữ nhật

Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
Do đó: AHCD là hình bình hành
Hình bình hành AHCD có\(\widehat{AHC}=90^0\)
nen AHCD là hình chữ nhật

có:
M là trung điểm của AC (gt)
D đối xứng H qua M(gt) => M là trung điểm của DH
Xét tứ giác AHCD có:
2 đường chéo cắt nhau tại trung điểm mỗi đường(cmt)
=> Tứ giác AHCD là hình chữ nhật
Nhớ tick cho mình nha


Xét tứ giác AHCD có
M là trung điểm của AC
M là trung điểm của HD
Do đó: AHCD là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật